Напряженное и деформированное состояние в точке

В предыдущем разделе рассматривалось одноосное растяжение или сжатие, т.е. внешняя сила действует строго по оси, направления элементарных сил, действующих на элементарных площадках, напряжений, параллельны оси стержня или перпендикулярны к поперечному сечению- это нормальные напряжения. Если внешняя сила будет направлена произвольно, то в теле возникнут разные напряжения: нормальные, касательные

Рис. 2.14

Напряжения на наклонной площадке.

Разрежем тонкую пластину, на которую действуют внешние силы, направленные параллельно ее граням, наклонным сечением и выделим из него элементарную треугольную призму (рис. 2.14).

Для того, чтобы эта призма находилась в равновесии, на ее гранях должны действовать напряжения:

нормальные (перпендикулярные граням) s_a; s_х; s_у;

касательные (параллельные граням) t_a; t_ху; t_ух.

Значения s_a, t_a не известны.

Проецируя силы, действующие на призму, последовательно на направления нормали и касательной к наклонной площадке, получим формулы для вычисления нормальных и касательных напряжений на наклонной площадке

s_a= s_хcos²a+ s_ysin²a+ t_xysin(2a), (2-58)

t_a= 0,5(s_y- s_x)sin(2a)+ t_xycos(2a). (2-59)

Если касательные напряжения равны нулю, то площадка называется главной. При этом из (2-59) получаем

2 t_xy /(s_x- s_y)= tg(2a). (2-60)

Так как период тангенса равен p, то существует два взаимно перпендикулярных направления, образующих с осью х углы a₀ и a₀+ p/2, где касательные напряжения равны нулю, а в плоском напряженном состоянии существуют два главных напряжения. Их можно найти из уравнения (2-58) при a= a₀ [1]

s_a= s_хcos²a₀ + s_ysin²a₀ + t_xysin(2a₀)= (s_х+ s_y)/2+ (s_х- s_y)/2+

+t_xysin(2a₀)= 0,5(s_х+ s_y)± 0,5[(s_х- s_y)²+ 4t²_xy]^1/2.

Откуда

s₁= 0,5(s_х+ s_y)+ 0,5[(s_х- s_y)²+ 4t ²_xy]^1/2, (2-61)

s₂= 0,5(s_х+ s_y)- 0,5[(s_х- s_y)²+ 4t ²_xy]^1/2. (2-62)

Заметим, что s₁> s₂.

Следовательно, плоское напряженное состояние в каждой точке тела может быть представлено как растяжение и сжатие в 2-х взаимно- перпендикулярных направлениях.

При этом отметим, что при плоском напряженном состоянии третье главное напряжение равно нулю s₃ = 0.

Сложив (2-61) и (2-62), получим выражение s₁+ s₂= s_х+ s_у,

из которого следует, что сумма нормальных напряжений на 2-х взаимно перпендикулярных площадках не зависит от угла их поворота.

Дифференцируя по углу (2-59) и приравнивая это нулю, найдем

tg(2a_t)= (s_y- s_x)/ t_xy (2-63)

Подставив это равенство в (2-59), после преобразований получим

t = ± 0,5[(s_x- s_y)²+ 4t²_xy]^1/2. (2-64)

Откуда следует, что при t_xy= 0 максимальные и минимальные касательные напряжения равны по модулю и отличаются знаками, т.е.

t _max= 0,5 ½ s₁- s₂ ½. (2-65)

Взаимное положение главных площадок и площадок с экстремальными касательными напряжениями определяется равенством

tg2a₀* tg2a_T= - 1. (2-66)

Выделим теперь в теле, на который действуют разные силы, куб и нанесем на его гранях напряжения (рис.2.15). На рис. 2.15,а стороны куба параллельны координатным осям и здесь действуют нормальные и касательные напряжения. Поскольку тут имеются одинаковые парные составляющие, то в ряде случаев для изучения напряженного состояния выделяют пирамидку, а на ней- 6 компонентов сил. При этом само напряженное состояние оценивают тензором

s_x t_yx t_zx

Т= t_xy s_y t_zy (2-67)

t_xz t_yz s_z.

Тензор в отличие от вектора не имеет простого геометрического толкования. Его обычно задают в виде матрицы.

Из предыдущего следует, что, повернув некоторым образом куб, можно получить такое напряженное состояние, когда касательных напряжений не будет, а останутся лишь главные напряжения (рис. 2.15,б). В этом случае каждое из напряжений в соответствии с законом Гука будет приводить к продольной относительной деформации в.

а) б)

Рис. 2.15 Объемное напряженное состояние.

направлении его вектора e _{i j}= s _i/ E и поперечной для двух других направлений e _{j i} = -cs _j/Е

Таким образом, относительные деформации в объемном напряженном состоянии равны

e₁= Е^-1[s₁ - c(s₂ + s₃)], (2-68)

e₂= Е^-1[s₂ - c(s₁ + s₃)], (2-69)

e₃= Е^-1[s₃- c(s₂ + s₁)], (2-70)

Заметим, что s₁ > s₂ > s₃.

Уравнения (2-68)...(2-70) представляют собой закон Гука для объемного напряженного состояния.

Так как объем параллелепипеда равен V= abc, то изменение объема будет

DV= (¶V/¶a)Da+ (¶V/¶b)Db + (¶V/¶c)Dc = bcDa+ acDb+ baDc,

а относительное изменение объема

e_V= DV/ V= Da/a+ Db/b+ Dc/c= e₁ + e₂ + e₃. (2-71)

С учетом (2-68)....(2-70) относительное изменение объема будет

e_V= (1-2c)Е^-1(s₁ + s₂ + s₃). (2-72)

Если при одноосной деформации потенциальная энергия, накопленная единицей объема равна E_p1= 0,5s₁e₁, то при объемном напряженном состоянии

E_p3= 0,5(s₁e₁+ s₂e₂ + s₃e₃ ). (2-73)

Теории прочности

Для оценки прочности деталей применяют 4 теории прочности:

1. Теория наибольших нормальных напряжений.

Здесь развиваемые нормальные напряжения не должны превышать допускаемые значения, определяемые по специальным требованиям, т.е.

s £ [s].

2. Теория наибольших линейных деформаций, по которой деформации не должны превышать допускаемые значения, т.е.

e£ [e]; q£ [q].

3. Теория наибольших касательных напряжений, по которой опасное состояние для детали наступает тогда, когда наибольшее касательное напряжение достигает значения, при котором проявляется текучесть материала.

Условие прочности здесь записывается в форме

t_max£ t₀,

где t₀ - предельное значение касательного напряжения при кручении.

Применяя это условие для плоского напряженного состояния, получают в предельных случаях

s_экв= s₁- s₃£ s₀,

а учитывая (2-61), это условие принимает вид

s_экв= [(s_x - s_y )²+ 4t²_xy]^1/2. (2-74)

Часто s_у= 0, тогда будет

s_экв= [s_x + 4t²_xy]^1/2. (2-75)

4. Энергетическая теория прочности основана на предположении, что сложное напряженное состояние равноопасно с простым растяжением, если они имеют одинаковые удельные энергии изменения формы.

В общем случае деформации часть энергии расходуется на изменение объема, а часть на изменение формы.

Из этих предположений вытекают формулы

s_экв= s_i= 2^-1/2[(s_z- s_y)²+ (s_y- s_x)²+ (s_z- s_x)² + 6(t²_xy+ t²_zx+ t²_yz)]^1/2. (2-76)

e_i= [2^1/2 (1+c)] ^-1[(e_y- e_z)²+ (e_z- e_x)²+ (e_x- e_y)²+ 1,5(q ²_yz+ q ²_zx+q ²_xy)]^1/2 . (2-77)

Здесь буквами s_i , e_i обозначены, соотвественно, интенсивность напряжений и интенсивность деформаций; q_ij - относительный угол закручивания.

Эти формулы справедливы как для упругой, так и для пластичной деформации [3].

Исходя из этого, обобщенный закон Гука записывается в форме

s_i = E’e_i , (2-78)

где E’ - называется обобщенным модулем упругости, изменяющимся по мере деформации или в зависимости от действующих напряжений.

Для плоского напряженного состояния, когда s_z=0, t_zx= t_zу= 0 из (2-76) следует

s_i= 2^-1/2[ 2s_y²- 2s_ys_x+ 2s_x² + 6t²_xy]^1/2 = (s_y²- s_ys_x+ s_x ²+ 3t²_xy]^1/2. (2-79)

Если же имеет место одноосное напряженное состояние (s_x = 0), то получим

s_i= s_экв = (s² + 3t ²] ^1/2. (2-80)

Соотношение (2-80) используют в качестве условия возникновения пластических деформаций s_экв = s_т.

Если имеет место чистый сдвиг, то при s=0 из (2-80) получим касательное напряжение текучести

t_т= s_т / 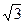. (2-81)

Заметим, что по 3-й теории прочности t_т= s_т /2.

Пример 2.2:

Определить запас прочности по пластической деформации болта М 24х1,5 при F₀= 45кН; М_кр= 200Нм; s_т = 650 МПа.

Внутренний диаметр резьбы d₁ = 22,38 мм. Тогда

продольные напряжения равны

s₁ = 4F₀ /(pd²₁)= 4*45000/(p22,38²)= 114,65 МПа;максимальные касательные напряжения (см. (2-96)) равны

t₁@ М_кр./(0,2 d³₁)= 200000/(0,2*22,38³)= 178,4 МПа.

Тогда

s_экв= s_i= (s²₁+ 3t²₁)^1/2= 325 МПа.

Запас по прочности будет n₁ = s_т/s_i= 650/325= 2.

Date: 2015-11-13; view: 750; Нарушение авторских прав