Матрицы одинакового размера считаются равными, если их соответствующие элементы равны

Матрица, все элементы которой нули, называется нулевой матрицей.

Произведением матрицы A = (a_ij) на число a называется матрица aА =(aa_ij), все элементы которой умножены на число a.

Суммой двух матриц одинаковых размеров А =(a_ij) _m´n, B =(b_ij) _m´n, называется матрица С = А + В = (a_ij + b_ij) _m´n тех же размеров, элементы которой равны суммам соответствующих элементов данных матриц.

Разность матриц А – В определяется равенством А – В = А +(-1) В.

Легко видеть, что справедливы соотношения:

1. a (А + В) = aА + aВ, 2. (a + β) А = aА + βА,

3. (a × β) А = a × (βА), где А, В – матрицы одного размера, a, β – числа.

Получаем следующий факт: совокупность матриц одного размера { A_m´n } есть линейное (векторное) пространство, обозначим его L_A ≡ L_Am´n = { A_m´n }.

Пример 1. Пусть: ,

тогда A+2B =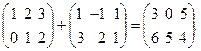

При m=n матрица A_n´n ≡ A _{( n )} называется квадратной порядка n.

Квадратную матрицу D = 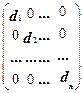, где d_i числа не все равные нулю, называют диагональной. Если d₁ = d₂ = … = d_n =1, то матрицу называют единичной и обозначают Е.

Произведением двух матриц специального размера A_m´r × B_r´n называется матрица C_m´n, у которой элемент c_ij, стоящий на пересечении i –ой строки и j -го столбца, равен скалярному произведению i -ой строки 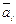матрицы А на j -й столбец матрицы В: C_m´n = A_m´r × B_{rх × n},

c_ij = 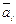× = a_i1b_1j + a_i2b_2j +…+ a_irb_rj

(i =1, 2, … m; j =1, 2, …, n).

Замечание 1. Операция умножения АВ двух матриц выполнима лишь в том случае, когда число столбцов первой матрицы А равно числу строк второй матрицы В.

Замечание 2. Умножение АВ выполнимо всегда, если матрицы квадратные одного порядка. Причем даже в этом случае может быть АВ ≠ ВА. Если АВ = ВА, то матрицы А и В называются перестановочными (коммутирующими). Естественно определяются степени матриц: A ² = A × A, A ³ = A × A × A = A ²× A.

Date: 2015-12-10; view: 274; Нарушение авторских прав