
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Евклидово n – мерное метрическое пространство Rn
|
|
Введем в векторном пространстве Аn скалярное произведение векторов  =(х1, х2, … хn),
=(х1, х2, … хn),  =(у1, у2, … уn) формулой:
=(у1, у2, … уn) формулой:
 ×
×  = х 1× у 1+ х 2· у 2+…+ xn · yn. (3)
= х 1× у 1+ х 2· у 2+…+ xn · yn. (3)
Из определения вытекают следующие свойства «скалярного умножения» для любых векторов  ,
,  ,
,  Î An и любого числа a Î R:
Î An и любого числа a Î R:
1.  ×
×  =
=  ×
×  ,
,
2. a  ×
×  = a
= a  ×
×  ,
,
3. ( +
+  )×
)×  =
=  ×
×  +
+  ×
×  .
.
Векторы  ,
,  называют ортогональными (перпендикулярными в случае n =2, n =3), если их скалярное произведение равно нулю:
называют ортогональными (перпендикулярными в случае n =2, n =3), если их скалярное произведение равно нулю:  ×
×  =0.
=0.
Длину вектора (норму вектора) в n - мерном пространстве определим величиной
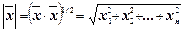 (4)
(4)

 Очевидно, каждый вектор
Очевидно, каждый вектор  ¹
¹  имеет положительную длину,
имеет положительную длину,  и лишь вектор-нуль
и лишь вектор-нуль  имеет длину, равную нулю:
имеет длину, равную нулю:  .
.
Евклидову метрику (расстояние) между точками (векторами),  ,
,  пространства An определим формулой:
пространства An определим формулой:
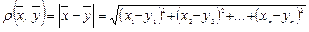 (5)
(5)
Это полный аналог расстояния в декартовой системе координат между точками на плоскости (n =2) или в пространстве (n =3).
Расстояние удовлетворяет аксиомам метрического пространства см. п. 2, § 2:
1. r ( ,
,  ) = 0 тогда и только тогда, когда
) = 0 тогда и только тогда, когда  =
=  ;
;
2. r ( ,
,  ) = r (
) = r ( ,
,  ) – свойство симметрии;
) – свойство симметрии;
3. если  = (z1, z2, …, zn) некоторая третья точка пространства, то справедливо неравенство треугольника:
= (z1, z2, …, zn) некоторая третья точка пространства, то справедливо неравенство треугольника:
r ( ,
,  ) ≤ r (
) ≤ r ( ,
,  )+ r (
)+ r ( ,
,  ).
).
Определение 2. Векторное пространство An с евклидовой метрикой (5) называется евклидовым n – мерным пространством Rn.
Вектор  называется нормированным (также единичным вектором) если
называется нормированным (также единичным вектором) если 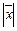 = 1. Для «нормировки» произвольного вектора
= 1. Для «нормировки» произвольного вектора  ≠
≠  достаточно умножить этот вектор на число l =
достаточно умножить этот вектор на число l =  :
: 
Примерами попарно ортогональных и нормированных векторов (ортонормированных) являются векторы  = (1, 0, …, 0),
= (1, 0, …, 0),  = (0, 1, …, 0), …,
= (0, 1, …, 0), …,  = (0, 0,…, 1).
= (0, 0,…, 1).
Любой вектор  = (х1, х2, …, хn)Î Rn можно представить линейной комбинацией векторов
= (х1, х2, …, хn)Î Rn можно представить линейной комбинацией векторов  ,
,  , …,
, …, 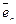 :
:
 = (х1, х2, …, хn) = х1 ×
= (х1, х2, …, хn) = х1 ×  + х2 ×
+ х2 ×  +…+ хn ×
+…+ хn × 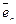 .
.
Пример 1. Скалярное произведение векторов  ,
,  из предыдущего примера 1, п. 1 равно
из предыдущего примера 1, п. 1 равно  ·
·  = (-2)·1+3·0+1·4+0·(-3)=2.
= (-2)·1+3·0+1·4+0·(-3)=2.
Длина (норма) вектора  равна ê
равна ê  ê=
ê=  =
=  , вектора 2
, вектора 2  –3
–3  равна │2
равна │2  –3
–3  │=
│=  =
= 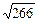 , последнее равносильно тому, что расстояние между точками пространства 2
, последнее равносильно тому, что расстояние между точками пространства 2  и 3
и 3  равно r (2
равно r (2  , 3
, 3  )=
)= 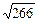 . Вектор
. Вектор  =
= 
 =
=  (-2, 3, 1, 0)=(
(-2, 3, 1, 0)=( 0) будет единичной длины, нормированным.
0) будет единичной длины, нормированным.
Date: 2015-12-10; view: 500; Нарушение авторских прав