Задача №1. Составление динамической модели рычажного механизма

Исходные данные для расчета: (необходимые для расчета данные выбираются из таблицы в соответствии с вариантом)

1. Угловая скорость кривошипа ω = 10 рад/с

2. Длина кривошипа i_АВ = 0,10 м

3. Относительная длина шатуна λ ⁼ 3,0

4. Отношение длин l_AE/l_AB = 0,2

5 Масса шатуна m₂ =2,0 кг

6. Масса ползуна m₃ = 3,0 кг

7. Сила, приложенная в т. С механизма f _c =100 Н
8. Сила, приложенная в т.Е механизма f_Е = 80 Н

Решение

1. Вычерчивается заданная схема данного механизма и его динамиче­ская модель На схеме показываются силы и моменты сил, приложенные к звеньям механизма.

Динамическая модель представляет собой условное звено, закон дви­жения которого совпадает с законом движения одного из звеньев механизма. В качестве динамической модели удобно принять ведущее звено АО

Чтобы выполнялось это равенство, при построении динамической мо­дели нужно учесть все силы и моменты, приложенные к звеньям механизма - заменить их действие приведенным суммарным моментом М

Массы всех звеньев (их инертности) учитываются суммарным приведенным момен­том I

2. Для механизма в заданном положении определяются линейные ско­рости всех точек звеньев, обозначенных на схеме механизма буквами, и уг­ловая скорость шатуна

Кинематическое исследование механизма начинается с ведущего звена.

Определяется скорость т. В

Скорость т С определяется по векторному уравнению:

где V_В- скорость т В, вычисленная по модулю и направленная перпенди­кулярно звену АВ в сторону вращения кривошипа,

V_CВ - скорость т С при вращении звена шатуна вокруг т В, перпенди­кулярная ВС, неизвестная по модулю (т к угловая скорость кри­вошипа неизвестна),

V_c - абсолютная скорость т С, направленная вдоль неподвижной на­правляющей (т е горизонтально), неизвестная по величине. Для решения векторного уравнения строится план скоростей.По­строение выполняется в следующей последовательности:

выбирается на чертеже произвольная точка p - полюс плана скоростей;

от полюса р строится вектор рb произвольной длины, изображающий скорость т. В, направленный перпендикулярно АВ в сторону вращения кри­вошипа;

через конец вектора рb проводится направление относительной ско­рости p а (перпендикулярно звену ВС),

в пересечении полученных направлений лежит т.cплана скоростей -конец вектора рс, изображающего скорость т С V_c в данном случае совпа­дает с т. b, следовательно V_C=V_B;

скорости точек S₂, S₃, D и Е определяются с использованием теоремы подобия, в соответствии с которой, точки на плане скоростей образуют фи­гуры, подобные фигурам, образованным соответственными точками на пла­не механизма. Так как точки S₂и D лежат на звене ВС, точки s₂ и d лежат на bc плана скоростей, т.е. совпадают с т. b и т. с. Точка S₃ (центр масс ползуна) совпадает с т. С.

Следовательно

Точка Е лежит на продолжении АВ Следовательно т е на плане скоро­стей лежит на продолжении ab, и вектор ре, изображающий скорость т Е V_E, выходит из полюса. Скорость т. Е определяется из соотношения.

или

где k_y, k, - соответственно масштабные коэффициенты плана скоростей и

плана механизма Тогда

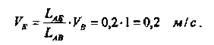
Точка А неподвижна, V_A = Q, следовательно т. а планаскоростей лежит в полюсе.

Угловая скорость шатуна:

3. Вычисляется суммарный приведенный момент всех сил и моментов сил, приложенных к звеньям механизма. Он определяется из условия равен­ства его работы сумме работ всех сил и моментов сил:

где i - номер точки приложения силы или звена, к которому приложен мо­мент

При <qa/=(hj'

Суммарный приведенный момент равен сумме приведенных моментов
и моментов сил, приложенных к звеньям механизма

Аналогично

Окончательно

Суммарный приведенный момент сил и моментов сил направлен в сто­рону, противоположную угловой скорости динамической модели, т.к для данного положения механизма он получился отрицательным.

4. Вычисляется суммарный приведенный момент инерции механизма Он определяется из условия равенства кинетических энергий - кинетическая энер­гия звена приведения равна сумме кинетических энергий звеньев механизма.

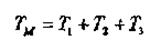
Квиетическая энергия звена i определяется по формуле

где т, - масса звена 1,

Va - скорость центра масс звена t,

1st - момент инерции звена i относительно оси, проходящей через

центр масс, ед - угловая скорость звена i

Первый член формулы выражает кинетическую энергию вращатель­ного движения звена, второй - поступательного Учитывая, что звено дина­мической модели совершает вращательное движение, второе звено движется плоско-параллельно, третье - поступательно, а также рекомендацию о том, что массой первого звена можно пренебречь, условие равенства кинетиче­ских энергий имеет вид

После подстановки суммарный приведенный

момент инерции вычисляется по формуле

ЗАДАЧА №2. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ МНОГОЗВЕННОГО ЗУБЧАТОГО МЕХАНИЗМА

Исходные данные для расчета (схема зубчатого механизма и числовые значения) выбираются в соответствии с вариантом.

Заданный многозвенный зубчатый механизм может быть представлен в де трех ступеней (ступени показаны на схеме пунктирными линиями) Передаточное отношение многозвенного механизма равно произведению пе­редаточных отношений ступеней.

Определяются передаточные отношения ступеней.

Первая ступень представляет собой планетарный механизм, переда­точное отношение которого находится по известной формуле

[1,2],

где U" - передаточное отношение обращенного механизма - механизма с

неподвижным водилом.

Передаточное отношение обращенного меха­низма равно произведению передаточных отноше­ний его ступеней

Передаточные отношения ступеней заменяю­щего механизма выражаются через числа зубьев с учетом знаков (- при внешнем зацеплении, + при внутреннем):,

Для решения необходимо предварительно найти Z₂, Zj*. Число зубьев третьего колеса вычисляется по заданным значениям передаточного отно­шения U₂₃ и числа зубьев Z₃

Планетарные механизмы конструктивно выполняются соосными, по­этому для определения числа зубьев второго колеса Zi может быть использо­вано условие соосности, которое выражается через межосевые расстояния и для данной схемы записывается!

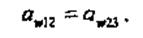
Так как в планетарных механизмах используются нулевые зубчатые колеса, межосевые расстояния могут быть выражены через радиусы дели­тельных окружностей

После подстановки в уравнение r = ~z, учитывая, что модули всех

колес одинаковые, условие соосности для данной схемы записывается

или 18 + Z₂=95-22.

Откуда

Передаточное отношение планетарного механизма

Вторая ступень представляет собой механизм, состоящий из трех зуб­чатых колес - Z4, Zs, Ze Передаточное отношение такого механизма опреде­ляется по формуле

Для этого механизма заданы передаточное отношение £/# и межосевое расстояние ацвд зубчатой пары Zj, Zs. Заданные параметры могут быть выра­жены через числа зубьев колес

или Совместное решение дает:

Число зубьев шестого колеса определяется из условия соосности, кото­рое для данного механизма имеет вид

Окончательно

Передаточное отношение второй ступени

Третья ступень состоит из зубчатых колес Z₇, Z₈, Z_s Числа зубьев колес этой передачи определяются следующим образом.

число зубьев Z$ вычисляется по заданным значениям Zp и С/да

число зубьев Z? определяется по вычисленному значению Za и задан­ному межосевому расстоянию aws

Z, = 18, передаточное отношение третьей ступени

передаточное отношение зубчатого механизма

ЛИТЕРАТУРА

1 Теория механизмов и механика машин Учебное пособие для втузов /KB Фролов, С.А. Попов, А К Мусатов и др/Под ред К В Фролова. - М Высшая школа, 1998 -496с

2 Артоболевский И.И Теория механизмов и машин - М Наука, 1975

Date: 2015-12-10; view: 925; Нарушение авторских прав