
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Механическое движение, Виды механического движения. Поступательное движение. Траектория. Путь. Перемещение. Скорость. Ускорение
|
|
Конспект лекция по физике и биофизике для студентов ФВМ НИСПО заочной формы обучения.
Составила к.б.н., доцент Соколовская Светлана Николаевна.
ЛЕКЦИЯ 1. МЕХАНИКА
Механическое движение и его виды. Путь, перемещение, скорость и ускорение при поступательном движении.
Вращение твердого тела относительно неподвижной оси. Угловая скорость и угловое ускорение.
Законы Ньютона в инерциальных системах отсчета.
Импульс тела. Закон сохранения импульса и примеры его применения.
Основное уравнение динамики вращательного движения твердого тела. Момент силы и момент инерции.
6. Силы в механике: сила тяжести, сила упругости, сила трения.
Деформация твердого тела. Закон Гука. Модуль Юнга. Упругие свойства тканей живых организмов.
Энергия. Кинетическая и потенциальная энергия. Закон сохранения энергии в механике. Работа и мощность. Работа постоянной силы. Работа и мощность животных и человека.
Колебательные движения в природе и в биологических объектах. Гармонические колебания и их характеристики.
Волны в упругих средах. Природа звука. Источники звука.
Механическое движение, Виды механического движения. Поступательное движение. Траектория. Путь. Перемещение. Скорость. Ускорение.
Механика- раздел физики изучающий механическое движение.
Механическим движением называется перемещение тел или их частей в пространстве относительно друг друга с течением времени. Механическое движение относительно, т.е. перемещение любого тела можно рассматривать только относительно других тел.
Раздел механики изучающий геометрические свойства движения называется кинематикой.
Тело, относительно которого рассматривается движение других тел, называется телом отсчёта.
Система отсчёта - это система координат, связанная с телом отсчёта и снабжённая часами.
Если форма и размеры тела не оказывают существенного влияния на характер его движения, то такое тело можно принять за материальную точку. Материальной точкой называется тело, формой и размерами которого в данной задаче можно пренебречь.
Существует три вида механического движения: поступательное, вращательное и колебательное.
Поступательным называется такое движение твёрдого тела, при котором все его точки описывают одинаковые траектории и движутся с одинаковыми скоростями и ускорениями в данный момент времени. Поэтому для описания его движения достаточно описать движение одной его точки.
Рассмотрим движение материальной точки относительно системы отсчёта, связанной с телом отсчёта 0 (рис. 1).
Линия, описываемая точкой при ее движении, называется траекторией. По виду траектории движения разделяются на прямолинейные и криволинейные.
Отрезок траектории АВ, пройденный точкой за некоторый промежуток времени ∆ t, представляет собой путь ∆s, а направленный отрезок  , соединяющий начальную точку с конечной, - перемещение ∆
, соединяющий начальную точку с конечной, - перемещение ∆ 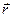 .
. 
Путь и перемещение измеряются в метрах. Путь ∆ s - величина скалярная, а перемещение ∆ 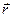 - векторная. При прямолинейном движении путь и перемещение совпадают, при криволинейном -
- векторная. При прямолинейном движении путь и перемещение совпадают, при криволинейном -  >∆ r.
>∆ r.
Величина, численно равная отношению перемещения ко времени, за которое это перемещение произошло, называется средней скоростью движения:
 . (1)
. (1)
 Средняя скорость измеряется в м/с, величина векторная. Вектор средней скорости совпадает по направлению с вектором перемещения (рис.1)
Средняя скорость измеряется в м/с, величина векторная. Вектор средней скорости совпадает по направлению с вектором перемещения (рис.1)
 z
z



 . В некоторых случаях вводится понятие средней скалярной скорости. Средняя скалярная скорость есть величина, численно равная отношению пути ко времени, за которое этот путь пройден:
. В некоторых случаях вводится понятие средней скалярной скорости. Средняя скалярная скорость есть величина, численно равная отношению пути ко времени, за которое этот путь пройден:
 (2)
(2)
y
X Рис. 1
Измеряется в м/с, величина скалярная. 
Движение материальной точки называется равномерным, если её скорость не изменяется с течением времени, в противном случае движение называется неравномерным. Быстрота изменения скорости характеризуется ускорением.
Пусть материальная точка переместилась за промежуток времени  t из точки А, где она имела скорость
t из точки А, где она имела скорость  , в точку В, где она имеет скорость
, в точку В, где она имеет скорость 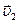 (рис.2). Изменение скорости
(рис.2). Изменение скорости 
 Средним ускорением называется величина, численно равная отношению изменения скорости ко времени, за которое это изменение произошло
Средним ускорением называется величина, численно равная отношению изменения скорости ко времени, за которое это изменение произошло
 (3)
(3)
Рис. 2
Измеряется в м/c2, величина векторная.
Вектор среднего ускорения направлен так же, как и приращение скорости  , то есть под углом к траектории в сторону её вогнутости (рис.2).
, то есть под углом к траектории в сторону её вогнутости (рис.2).
Из неравномерных движений, которые могут встречаться на практике, особый интерес представляет равнопеременное движение.
Равнопеременным называется движение, происходящее с постоянным ускорением. В этом случае мгновенное ускорение в любой момент времени равно среднему ускорению:

откуда
 (4)
(4)
где 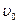 - начальная скорость,
- начальная скорость,
 - мгновенная скорость в любой момент времени.
- мгновенная скорость в любой момент времени.
Если 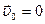 , то
, то  . (5)
. (5)
Перемещение равно  (6)
(6)
при 
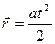 . (7)
. (7) 
- Вращательное движение. Угловое перемещение. Угловая скорость. Угловое ускорение.
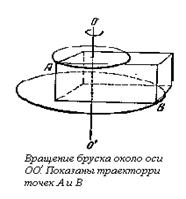 |  |
Вращательным движением твердого тела вокруг неподвижной оси называется такое движение, при котором все его точки описывают окружности, лежащие в параллельных плоскостях, с центрами на одной прямой, называемой осью вращения (рис. 1).
Рис.1 Рис.2
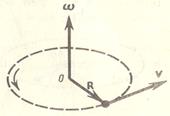
Рассмотрим движение одной точки вращения твердого тела. Пусть точка движется по окружности радиуса R (рис.2). За малый промежуток времени  линейное перемещение точки по окружности равно
линейное перемещение точки по окружности равно  . Тогда радиус-вектор
. Тогда радиус-вектор  точки повернулся на угол
точки повернулся на угол  . Угол поворота радиуса-вектора (угловое перемещение)
. Угол поворота радиуса-вектора (угловое перемещение)  измеряется в радианах (рад). Угловое перемещение
измеряется в радианах (рад). Угловое перемещение  связано с линейным перемещением
связано с линейным перемещением  соотношением
соотношением  .
.
Средней угловой скоростью называется величина, численно равная отношению угла поворота радиуса-вектора ко времени, за которое произошел этот поворот
 (1)
(1)
 Направление вектора угловой скорости определяется по правилу буравчика (правого винта) (рис.3). Рис.3
Направление вектора угловой скорости определяется по правилу буравчика (правого винта) (рис.3). Рис.3
Вектор угловой скорости совпадает по направлению с поступательным движением острия буравчика, рукоятка которого вращается в направлении движения точки по окружности.
Линейная скорость – это скорость, с которой точка движется по окружности. Измеряется в м/с. Вектор линейной скорости направлен по касательной к окружности, которую она описывает (рис.3).
Так как путь, пройденный точкой равен  то
то
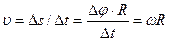 . (3)
. (3)
При неравномерном движении точки по окружности быстрота изменения угловой скорости характеризуется угловым ускорением.
Если за промежуток времени  угловая скорость изменилась на
угловая скорость изменилась на  , то среднее угловое ускорение
, то среднее угловое ускорение
 (4)
(4)
Среднее угловое ускорение есть величина, численно равная отношению изменения угловой скорости ко времени, за которое это изменение произошло.
При ускоренном вращении вектор углового ускорения  совпадает по направлению с вектором угловой скорости
совпадает по направлению с вектором угловой скорости 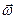 , при замедленном вращении – противоположен ему (рис.4).
, при замедленном вращении – противоположен ему (рис.4).

Линейное ускорение есть величина, численно равная отношению изменения линейной скорости ко времени, за которое это изменение произошло
 (5)
(5)
Рис.4
Линейное ускорение точки связано с угловым ускорением соотношением
 (6)
(6)
где R – радиус окружности, описываемой этой точкой.
Т.к. при вращательном движении твердого тела угловые скорости и угловые ускорения всех его точек одинаковы в данный момент времени, то вращательное движение твердого тела можно характеризовать угловой скоростью и угловым ускорением любой его точки.
Рассмотрим равнопеременное вращение тела, то есть вращение с постоянным угловым ускорением. В этом случае мгновенное ускорение в любой момент времени равно среднему

откуда  . (7)
. (7)
Если  то
то  (8)
(8)
Угол поворота тела при равноускоренном вращательном движении можно определить по формуле:
 .(9)
.(9)
При 
 . (10)
. (10)
- Законы Ньютона в инерциальных системах отсчёта. Импульс тела. Закон сохранения импульса изолированной системы.
В кинематике не рассматривали взаимодействия тел, однако все изменения движения происходят благодаря взаимодействию тел друг на друга.
Раздел физики изучающий взаимодействие тел называется динамикой.
В основе динамики лежат три закона Ньютона (сформулированы в 1687 году в труде великого ученого «Математическое начало натуральной философии», этот труд явился обобщением опытных и теоретических закономерностей установленных Ньютоном, Кеплером, Галилеем и Гуком).
1-вый закон Ньютона Всякое тело сохраняет состояние покоя или прямолинейного равномерного движения до тех пор, пока внешние тела не воздействуют на это тело. Система отсчета в которой выполняется этот закон называются инерциальными.
2-вый закон Ньютона Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила  а также способы их измерения. Первая из этих величин – масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила
а также способы их измерения. Первая из этих величин – масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила  – является количественной мерой действия одного тела на другое.
– является количественной мерой действия одного тела на другое.
Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

|
2. Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:

|
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:
|
Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила  :
:

|
В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2. Эта единица называется ньютоном (Н).
3-вый закон Ньютона:
|
Это равенство называется третьим законом Ньютона.
Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
Date: 2015-12-10; view: 2084; Нарушение авторских прав

