
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод найменших квадратів
|
|
При вивченні закономірностей в деяких дослідженнях інженерної справи, економіки, біології, медицини і т.п. приходиться аналітично описувати (у вигляді формули) зв'язок між двома змінними x та y. Для цього в процесі експериментів, спостережень вимірюють з можливою точністю окремі значення xi і відповідні їм значення yi (i=1,2,…,n), або отримують такі значення як статистичні дані. В результаті маємо таблицю значень (табл. 1).
Таблиця 1
| x | x1 | x2 | … | xi | … | xn |
| y | y1 | y2 | … | yi | … | yn |
 |
Подібну таблицю можна отримати, наприклад, при дослідженні лінійного розширення стержня в залежності від температури, якщо коефіцієнт лінійного розширення данного матеріалу невідомий, тоді x1, x2,…, xn – виміряні значення температури, а y1, y2,…,yn – відповідні їм значення довжини.
Побудуємо у вибраній системі координат XOY точки Mi(xi, yi), координати яких відповідають даним таблиці 1 (див. рис. 1).
Тепер виникає необхідність вибору відповідної функції y=f(x), яка б описувала зв'язок між x і y. Таку функцію називають емпіричною. В загальному випадку вибір емпіричної функції не є однозначним. Можна знайти лінію, яка б проходила через кожну з точк Mi, це може бути так званий інтерполяційний многочлен (на рис. 1 це пунктирна лінія), порядок якого буде досить високим (на одиницю меншим, ніж кількість точок в таблиці). Крім того, дані таблиці 1 можуть бути не досить точними внаслідок наявності похибок вимірювання, а також впливу інших факторів, які ми не завжди можемо врахувати. Тому дослідники віддають перевагу більш простим і зручнішим функціям, таким, як лінійна  , квадратична
, квадратична  , показникова
, показникова
 , гіперболічна
, гіперболічна  і ін. Вибрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той чи інший метод вибору емпіричної залежності
і ін. Вибрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той чи інший метод вибору емпіричної залежності
 (на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри вибраної залежності
(на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри вибраної залежності 
Позначимо через  відхилення емпіричної функції в точці
відхилення емпіричної функції в точці  від відповідного табличного (експериментального) значення
від відповідного табличного (експериментального) значення  . Зрозуміло (див. рис. 1), що
. Зрозуміло (див. рис. 1), що 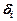 можуть бути для одних
можуть бути для одних  додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин
додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин  але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому
але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому 
Параметри функції  вибирають так, щоб сума квадратів S приймала найменше значення.
вибирають так, щоб сума квадратів S приймала найменше значення.
10. Розглянемо випадок, коли  лінійна функція з невідомими параметрами a i b. Тоді величина відхилення
лінійна функція з невідомими параметрами a i b. Тоді величина відхилення
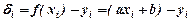 , а сума їх квадратів
, а сума їх квадратів
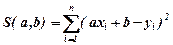 (14.1)
(14.1)
є функцією двох змінних a i b (xi, yi – це числа із таблиці 1). Відомо, що S (a,b) приймає мінімальне значення при тих значеннях a i b, при яких частинні похідні по цих змінних дорівнюють нулю, тобто коли

Із (14.1) знаходимо: 
Прирівнюючи до нуля частинні похідні, отримуємо систему рівнянь:
 (14.2)
(14.2)
Система (14.2) називається нормальною системою методу найменших квадратів.
Розв'язуючи систему рівнянь (14.2), знаходимо числа a i b, які підставляємо в рівняння 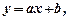 що і дає формулу шуканої залежності.
що і дає формулу шуканої залежності.
Отже під "найкращим" згладжуванням експериментальних даних в даному випадку вважається лінійна функція, параметри якої знайдені за методом найменших квадратів.
Метод найменших квадратів був запропонований німецьким математиком К. Гауссом.
Приклад 1. З різних дільниць шахт у вигляді таблиці отримані середні дані за квартал про залежність між собівартістю 1 тони залізної руди (в грошових одиницях) і глибиною добування (розробки, в метрах) (табл.2).
Таблиця 2
| x – глибина в метрах | |||||||
| y – грошова одиниця | 3,75 | 3,80 | 3,85 | 3,90 | 3,95 | 4,20 | 4,60 |
Припускаючи, що між змінними x i y існує лінійна залежність, знайти емпіричну формулу  за методом найменших квадратів.
за методом найменших квадратів.
Розв'язання. Для зручності побудуємо обчислювальну таблицю (табл. 3).
Таблиця 3
| № п/п | xi | yi | xiyi | xi2 |
| 1. | 3,75 | 1312,5 | ||
| 2. | 3,80 | 1444,0 | ||
| 3. | 3,85 | 1540,0 | ||
| 4. | 3,90 | 1638,0 | ||
| 5. | 3,95 | 1777,5 | ||
| 6. | 4,20 | 2100,0 | ||
| 7. | 4,60 | 2415,0 | ||
| cуми | 28,05 |
За значеннями сум таблиці складаємо нормальну систему методу найменших квадратів:

Зауважимо при цьому, що кількість точок в таблиці n=7.
Систему розв'яжемо за формулами Крамера




Таким чином, емпірична формула залежності між глибиною розробки і собівартістю однієї тони залізної руди має такий вигляд:
 Із формули видно, що із збільшенням глибини розробки на 100 метрів собівартість 1 тони залізної руди в середньому зростає на
Із формули видно, що із збільшенням глибини розробки на 100 метрів собівартість 1 тони залізної руди в середньому зростає на  грошової одиниці.
грошової одиниці.
Тепер згідно емпіричної формули обчислимо для відповідних значень xi теоретичні значення y(xi) і для порівняння заповнимо нову таблицю значень (табл. 4).
Таблиця 4
| xi | |||||||
| yi | 3,75 | 3,80 | 3,85 | 3,90 | 3,95 | 4,20 | 4,60 |
| y(xi) | 3,62 | 3,78 | 3,87 | 3,96 | 4,09 | 4,31 | 4,41 |
Для більшої наочності побудуємо в системі координат XOY точки за даними таблиці 4 і пряму лінію  Точки (xi,y(xi)) належать прямій лінії, а точки (xi, yi) на графіку (позначені кружочками) розміщені вздовж лінії з певними відхиленнями від прямої.
Точки (xi,y(xi)) належать прямій лінії, а точки (xi, yi) на графіку (позначені кружочками) розміщені вздовж лінії з певними відхиленнями від прямої.
 |
20. Зглажування квадратичною функцією 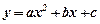 експериментальних даних. Зауважимо, що метод найменших квадратів застосовується для знаходження параметрів після того, коли вигляд функції y=f(x) встановлений. Але якщо з теоретичних міркувань неможна зробити певного висновку, якою повинна бути емпірична формула, то її вигляд наочно визначають із графічних зображень експериментальних даних. Так із рис. 1 суцільна лінія, яка проходить поміж точок M1, M2, M3,…,Mi,…,Mn нагадує параболу
експериментальних даних. Зауважимо, що метод найменших квадратів застосовується для знаходження параметрів після того, коли вигляд функції y=f(x) встановлений. Але якщо з теоретичних міркувань неможна зробити певного висновку, якою повинна бути емпірична формула, то її вигляд наочно визначають із графічних зображень експериментальних даних. Так із рис. 1 суцільна лінія, яка проходить поміж точок M1, M2, M3,…,Mi,…,Mn нагадує параболу  Тому у випадку квадратичної функції знаходимо мінімум суми
Тому у випадку квадратичної функції знаходимо мінімум суми  як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю

Знаходимо частинні похідні:

Прирівнюючи кожну з похідних до нуля отримуємо систему лінійних відносно a, b, c рівнянь:
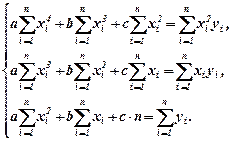 (14.3)
(14.3)
Приклад 2. Застосовуючи метод найменших квадратів знайти значення параметрів функції  якщо відомі такі значення змінних (див. табл. 5).
якщо відомі такі значення змінних (див. табл. 5).
Таблиця 5
| x | 0,5 | 1,5 | 2,5 | ||
| y | 0,8 | 1,9 | 4,9 | 8,8 | 13,9 |
Розв’язання. Для наочності побудуємо точки за даними таблиці 5 в системі XOY (див. рис.3), розміщення яких нагадує параболу, для знаходження параметрів якої заповнюєм обчислювальну таблицю 6.
Таблиця 6
| № п\п | xi | yi | xi2 | xi3 | xi4 | xiyi | xi2yi |
| 1. | 0,5 | 0,8 | 0,25 | 0,125 | 0,0625 | 0,4 | 0,2 |
| 2. | 1,0 | 1,9 | 1,0 | 1,0 | 1,0 | 1,9 | 1,9 |
| 3. | 1,5 | 4,9 | 2,25 | 3,375 | 5,0625 | 7,35 | 11,025 |
| 4. | 2,0 | 8,8 | 4,0 | 8,0 | 16,0 | 17,6 | 35,2 |
| 5. | 2,5 | 13,9 | 6,25 | 15,625 | 39,0625 | 34,75 | 86,875 |
| суми | 7,5 | 30,3 | 13,75 | 28,125 | 61,1875 | 62,0 | 135,2 |
Підставляючи значення сум із табл.6 в (14.3) отримуємо лінійну систему рівнянь відносно параметрів a, b, c:
 (14.4) Систему (14.4) можна розв'язати, наприклад, шляхом виключення невідомої
(14.4) Систему (14.4) можна розв'язати, наприклад, шляхом виключення невідомої  з наступним розв'язуванням нової системи відносно
з наступним розв'язуванням нової системи відносно 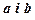 . Наводимо готові результати:
. Наводимо готові результати: 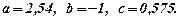 Шукана функція матиме вигляд:
Шукана функція матиме вигляд: 

Рис.3
30. Вирівнювання дослідних даних за гіперболою 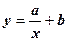 здійснюється за допомогою заміни
здійснюється за допомогою заміни  В такому разі в таблицю значень потрібно доповнити значеннями
В такому разі в таблицю значень потрібно доповнити значеннями 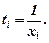
Таблиця 7

| 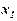
| 
| … | 
| … | 
|

| 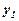
| y2 | … | 
| … | 
|

| 
| 
| … | 
| … | 
|
Після цього знаходиться мінімум функції 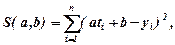 яка має такий же вигляд, як функція (14.1), і тому відповідна система запишеться:
яка має такий же вигляд, як функція (14.1), і тому відповідна система запишеться:
 (14.5)
(14.5)
Для отримання системи (14.5) складається відповідна обчислювальна таблиця відносно значень 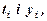 з якої знаходять
з якої знаходять
необхідні для системи суми. Після знаходження 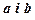 отримуємо функцію
отримуємо функцію 
40. Вирівнювання дослідних даних за показниковою функцією
 здійснюється за допомогою логарифмування
здійснюється за допомогою логарифмування 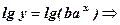
 і подальшою заміною
і подальшою заміною 
 Тоді отримаємо лінійну залежність
Тоді отримаємо лінійну залежність 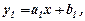 параметри якої
параметри якої  знаходимо за розглянутим вище методом найменших квадратів.
знаходимо за розглянутим вище методом найменших квадратів.
Приклад 3. За даними таблиці 8 знайти параметри залежності

Таблиця 8
| x | |||||
| y |
Розв'язання. Побудуємо точки відповідно таблиці 8 (див. рис.4).

Рис.4
Складаємо обчислювальну таблицю
Таблиця 9
| № п/п | xi | yi | y1=lgy | xiy1,i | xi2 |
| 1. | |||||
| 2. | 2,1847 | 8,7388 | |||
| 3. | 2,3600 | 18,8787 | |||
| 4. | 2,4771 | 29,7255 | |||
| 5. | 2,5611 | 38,4165 | |||
| суми | 11,5829 | 95,7595 |
За даними сум таблиці 9 маємо систему:

для якої знаходимо визначники

Згідно формул Крамера знаходимо 

Отже маємо лінійну функцію 
Поскільки  то
то 
 Таким чином, відповідно до таблиці 8 і рис. 4 ми знайшли показникову залежність
Таким чином, відповідно до таблиці 8 і рис. 4 ми знайшли показникову залежність 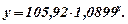
Date: 2015-12-10; view: 1041; Нарушение авторских прав