Скалярне поле. Похідна за напрямом. Градієнт

Означення 10.1. Скалярним полем називається область, в кожній точці якої задано деяку скалярну величину.

Прикладами скалярних полів є поле температур, тиску. Щоб задати скалярне поле, досить визначити відповідну функцію. В R² це u(x,y), в R³ – u(x,y,z). Для наглядності сприйняття скалярного поля в двовимірному випадку вводять лінії рівня, які є лініями перетину поверхні u=u(x,y), що визначає поле, і площини u=C. Рівняння ліній рівня в площині XoY є u(x,y)=C.

Для тривимірного поля u(x,y,z) маємо поверхні рівня, які задаються рівнянями:

u(x,y,z)=С.

В одновимірному випадку похідна функції характеризує швидкість зміни функції в даній точці в напрямі осі оХ. Розглянемо швидкість зміни функції u=u(x,y,z) в довільному напрямі. Нехай скалярне поле визначається функцією u=u(x,y,z) в деякій області, що містить точку М_о(x_о ,y_о ,z_о ). Через цю точку проходить пряма l, напрям якої визначається вектором . Тоді напрямні косинуси запишуться:

де - кути між і координатними осями.

Рівняння прямої l в параметричному виді має вигляд:

Тоді функція u в напрямку прямої l запишеться так:

.

Похідна функції за даним напрямом в точці М_о(x_о ,y_о ,z_о ) знахо-диться як похідна по параметру t:

(10.1)

Розглянемо вектори:

і ,

тоді похідна за даним напрямом в точці М₀(x₀ ,y₀ ,z₀ ) має вигляд:

(10.2)

Враховуючи, що , маємо:

.

Тоді

.

Таким чином, похідна (10.2) набуває максимуму, коли 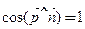, або , тобто, коли за напрям l взяти напрям вектора , який називається градієнтом функції u=u(x,y,z) в точці М₀(x₀ ,y₀ ,z₀ ), що визначається:

grad ,

або

grad 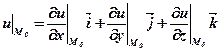(10.3)

Ще одна властивість градієнта полягає в тому,що градієнт поля в даній точці нормальний до лінії рівня поля в цій точці. Очевидно, модуль градієнта дорівнює:

.

Приклад 10.1. Лінії рівня функції функції - це еліпси . Маємо , і градієнт:

ортогональний дотичним на лінії рівня.

Лінії рівня функції u(x,y) і градієнти показані на рис.10.1.

Рис.10.1.

Date: 2015-12-10; view: 604; Нарушение авторских прав