Приведение квадратичной формы к каноническому виду в евклидовом пространстве

Рассмотрим два способа приведения квадратичной формы к каноническому виду:методом Лагранжа и с помощью ортогонального преобразования базиса, индуцированного собственными векторами симметрического оператора .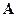

Пример 1. Привести квадратичную форму к каноническому виду: q (

Применим метод Лагранжа, который основан в выделении полного квадрата.

Вначале выделим полный квадрат при переменной 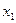, коэффициент которого отличен от нуля:

Обозначим: .

Теперь выделяем полный квадрат при переменной , коэффициент при которой отличен от нуля:

+

Обозначим: Тогда q канонический (нормальный) вид, полученный при переходе к новому базису, где формулы преобразования координат определяются системой

Замечание. Можно найти и другой базис, где q (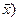 также имеет каноническую форму.

Оператор 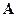в евклидовом пространстве называется симметрическим (самосопряженным), если для любых :

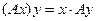
Очевидно, что 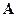– симметрический оператор тогда и только тогда, когда в ортонормированном базисе пространства его матрица А – симметрическая.

Примем без доказательства следующее утверждение.

Теорема. Для симметрического оператора 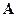в евклидовом пространстве существуют попарно ортогональные собственные векторы оператора 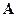и соответствующие им собственные значения действительные числа, т.е. матрица А имеет диагональный вид: А= , где .

Тогда всякая симметрическая билинейная форма задается формулой , где – матрица симметрического оператора 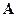. С другой стороны , значит, для того чтобы представить квадратичную форму в канонической форме, достаточно привести матрицу А соответствующегосамосопряженного оператора 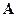к диагональному виду, используя ортогональные преобразования ортонормированного базиса в . Следует заметить, что приведение к нормальному виду требует перехода к аффинному базису.

Пример2. Привести к каноническому виду квадратичную форму и найти ортогональное преобразование, приводящее квадратичную форму к этому виду.

Запишем матрицу квадратичной формы , находим собственные значения G.

,

. Значит, квадратичная форма имеет канонический вид .

Переходим к нахождению базиса, для этого находим собственные векторы, решая систему

1) ,

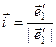Находим частное решение этой системы:(-1,2,1), откуда и , . Значит, .

Далее находим , , соответствующие собственному значению .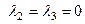

.

Одним из частных решений является , тогда . Координаты вектора должны удовлетворять уравнению , и вектор должен быть ортогонален . Значит, координаты являются решениями системы 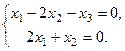Частное решение этой системы определяет вектор , тогда . Используя найденные векторы , записываем формулы преобразования координат при переходе от базиса к новому базису :

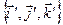Литература

1. Александров П.С. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1979.

2. Атанасян Л.С.,Базылев В.Т. Геомертия. В 2-х ч.Ч.1-М.: Просвещение,1986.

3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1984.

4. Бортаковский А.С.,Пантелеев А.В. Линейная алгебра в примерах и задачах. –М.:Высшая школа,2005.

5. Воеводин В.В. Линейная алгебра.-М.: Наука, 1980.

6. Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, 1984.

7. Клетеник Д.В. Сборник задач по аналитической геометрии. - М.: На ка,1964.

8. Кострикин А.И. Введение в алгебру. Основы алгебры. - М.: Физмат­лит, 1994.

9. Курош А.Г. Курс высшей алгебры. - М.: Наука,1965.

10. Ланкастер П. Теория матриц. - М.: Наука, 1988.

11. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И. Ермакова. - М.: ИНФРА-М, 2003.

12. Окунев Л.Я. Высшая алгебра. - М.: Просвещение, 1966.

13. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1978.

14. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича. - М.: Наука, 1981.

15. Сборник задач по геометрии: Учебное пособие. 2-е изд.,стер./Под ред. В.Т.Базылева. –СПб.: Издательство «Лань», 2008.

16. Шипачев В.С. Основы высшей математики. - М.: Высшая школа, 1994.

17. Фаддеев Д.К, Соминский И.С. Сборник задач по высшей алгебре. - М.: 1977.

Date: 2015-12-10; view: 1066; Нарушение авторских прав