Квадратичные формы

При решении многих задач приходится исследовать квадратичную форму: q (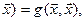 где g симметрическая билинейная форма векторного пространства .

Очевидно, что зная квадратичную форму, можно восстановить соответствующую билинейную форму g:

g( .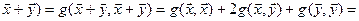

Таким образом, в некотором базисе 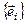симметрическая матрица G билинейной формы определяет не только билинейную форму, но и квадратичную форму (верно и обратное):

q(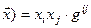 (1)

или то же самое в матричной форме:

q (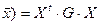. (2)

Совершим замену базиса 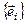на базис 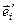, используя матрицу перехода ,: 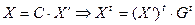. Подставив в (2), в новом базисе имеем: q (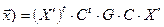,то есть в новом базисе матрица 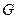квадратичной формы g имеет вид:

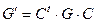(3)

Если при этом матрица примет диагональный вид, то говорят, что квадратичная форма приведена к каноническому виду:

q ( (4)

Рангом квадратичной формы g(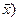 называется ранг матрицы G.

В силу (3) ранг квадратичной формы не меняется при переходе к новому базису, т.к. матрицы и С – невырожденные. Квадратичная форма g 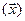называется невырожденной, если ее ранг равен размерности векторного пространства, в противном случае – вырожденной.

Теорема. В векторном пространстве всегда существует такой базис, в которой квадратичная форма (1) имеет канонический вид:

q (, (5)

где r – ранг канонической формы.

В силу теоремы § 36 существует базис 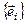в котором квадратичная форма g(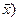 имеет канонический вид (4), ее матрица примет диагональный вид:

G=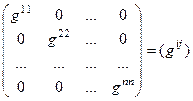

Так как квадратичная форма q имеет ранг r, то точно r коэффициентов 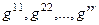отличны от нуля, а остальные равны нулю. Поэтому имеем

q (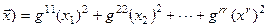

Следует заметить, что некоторые из коэффициентов 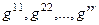могут быть отрицательными.

Нормальной формой q (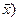 называется ее представление в виде: q ( (6)

Нормальная форма получена из канонической путем перехода к новому неортонормированному базису 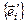,где .

Число отрицательных коэффициентов в представлении (6) называется индексом этой квадратичной формы, обозначим его h.

Разность между числом положительных и числом отрицательных коэффициентов называется сигнатурой этой формы.

Имеется следующее утверждение (закон инерции), которое приведем без доказательства.

Теорема. Индекс(сигнатура) квадратичной формы не зависит от выбора базиса, в котором она имеет нормальный (канонический) вид.

Квадратичная форма q (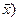 является положительно (отрицательно) определенной, если для любого 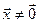выполняется q (.

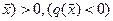Очевидно, для того чтобы q 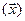была положительно определенной, необходимо и достаточно, чтобы все коэффициенты 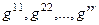канонической формы были положительными.

Для определения знакоопределенности квадратичной формы q (, без приведения к канонической форме, можно применить критерий Сильвестра: для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы G=(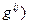 были положительными, т.е

(

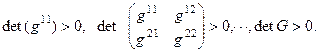
Date: 2015-12-10; view: 453; Нарушение авторских прав