Евклидово пространство

Билинейной формой g на называют билинейное отображение g: R.

Билинейность означает линейность по каждому аргументу:

g(

g (

для любых 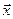из и из R.

Пусть 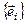, i = 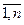- базис , то

Тогда g( обозначим g(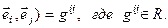 Тогда

g(. (1)

В этой записи учтена краткая запись суммы: если некоторый индекс встречается дважды: один раз – вверху и один раз – внизу,- то по этому индексу подразумевается суммирование.

Таким образом, если в выбран базис, то каждая билинейная форма g определяет квадратную матрицу G= .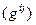

Верно и обратное: каждая квадратная матрица G определяет некоторую билинейную форму g. Поэтому матрицу G называют матрицей билинейной формы.

Билинейная форма g называется симметрической, если для любых т.е

g –симметрическая билинейная форма тогда и только тогда, когда матрица G-симметрическая, т.е G= .

Симметрическую билинейной форму называют положительно определенной, если для всякого вектора выполняется: g( >0.

Например, билинейная форма g, определяемая единичной матрицей G=E, g( – положительно определенная. Действительно, g(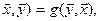 то есть g-симметрическая, а также g( >0, где учтено, что

Ненулевые векторы 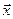и называются сопряженными относительно билинейной формы g, если g(.

Теорема. В любом векторном пространстве существует хотя бы один базис, любые два вектора которого сопряжены относительно данной симметричной билинейной формы g.

Векторное пространство называется евклидовым векторным пространством, если в нем определена положительно определенная билинейная форма g, при этом g( называется скалярным произведением векторов 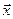и , пишут

или

Положительно определенная билинейная форма g удовлетворяет известным свойствам скалярного произведения векторов:

1)

2)

3)

4) >0, где скалярный квадрат вектора

Эти свойства (очевидны из определения g) являются аксиомами для аксиоматического определения скалярного произведения векторов. Покажем, что если g положительно определенная билинейная форма, то

g(

Для этого докажем в введенных обозначениях, что:

-1 (2)

Из условия положительной определенности g имеем: .

Поэтому число определяет косинус угла между векторам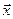и и : то есть cos что и требовалось доказать.

Согласно определению, базис 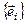является ортонормированным, если векторы единичны и взаимноперпендикулярны в евклидовом пространстве . Утверждается, что в евклидовом пространстве существует ортонормированный базис.

Действительно, пусть cопряженный базис относительно g, то искомый базис определяется векторами: .

Очевидно, что в ортонормированном базисе положительно определенная билинейная форма g определяется единичной матрицей, то есть 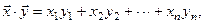и

cos

Date: 2015-12-10; view: 390; Нарушение авторских прав