Поверхности вращения

Поверхность, которая вместе с каждой своей точкой содержит всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой, называется поверхностью вращения.

Прямая d, вокруг которой производится вращение, называется осью вращения. В сечении поверхности вращения плоскостями, перпендикулярными оси вращения, получаются окружности, которые называются параллелями. Плоскости, проходящие через ось вращения, пересекают поверхность вращения по линиям, называемыми меридианами.

Поверхность вращения может быть образованаследующим образом. Пусть в плоскости П даны прямая d и линия 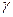. Поверхность, образованная вращением линии 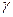вокруг прямой d, есть поверхность вращения с осью вращения d. Каждая точка линии 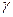, вращаясь вокруг прямой d, описывает окружность с центром на оси (параллель этой поверхности).

Поверхностью вращения второго порядка называется поверхность, образованная вращением линии второго порядка вокруг ее оси симметрии (исследовать методом сечения):

– эллипсоид вращения,

– однополостный гиперболоид вращения,

– двуполостный гиперболоид вращения,

– параболоид вращения

Пусть даны плоскость П и вещественное число . Рассмотрим отображение f пространства в себя по закону: , где , а P - ортогональная проекция точки M на плоскость П.

Это преобразование называется сжатием пространства к плоскости П, а число k называется коэффициентом сжатия.

Возьмем ортонормированный репер и найдем формулы сжатия f пространства к плоскости (Oxy), если дан коэффициент сжатия k. Пусть точки M и в репере R имеют координаты M(x,y,z), . Из определения сжатия

следует: , , .

Аналогично, получаем формулы сжатия к плоскости (Oxz):

, , ,

к плоскости (Oуz): , , .

Поверхности второго порядка получаются из поверхности вращения второго порядка с помощью сжатия к плоскости, проходящей через ось вращения.

Эллипсоидом называется поверхность , в которую переходит эллипсоид вращения F при сжатии к плоскости П, проходящей через ось вращения поверхности F,

Эллипсоид вращения F в репере определяется уравнением: .Совершив сжатие f к плоскости (Oyz) по формулам , , ,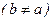получим уравнение эллипсоида в репере R:

.

Обозначим координаты текущей точки поверхности - через x,y,z и запишем уравнение эллипсоида в виде:

.

Аналогично могут быть получены следующие поверхности:

– однополостный гиперболоид,

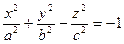– двуполостный гиперболоид,

–э ллиптический параболоид.

Гиперболическим параболоидом называется поверхность, определяемая каноническим уравнением: .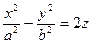

Изучим форму гиперболического параболоида методом сечений. Если поверхность, заданную в репере уравнением, пересечь плоскостью , то проекция сечения на плоскость в репере имеет уравнение:

Возможны три случая.

1). >0. Линия является гиперболой с вещественной осью (Ox). Следовательно, и равная ей линия пересечения поверхности с плоскостью , >0, является гиперболой, вещественная ось которой параллельна оси (Ox).

2). h=0. Плоскость (плоскость (Oxy)) пересекает поверхность по паре прямых: , , пересекающихся в вершине поверхности.

3). <0. Как и в случае 1), получаем, что сечением поверхности плоскостью является гипербола, но действительная ось гиперболы параллельна оси .

Если поверхность пересечь плоскостью , то в сечении получим параболу 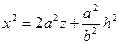. Следовательно, все эти параболы при изменении равны между собой и равны параболе , полученной в сечении поверхности координатной плоскостью . Оси этих парабол имеют положительное направление, определяемое вектором .

Аналогично убеждаемся, что в сечении поверхности плоскостью получаем параболу. Все такие параболы при изменении равны параболе , которая получается в сечении поверхности плоскостью .Оси этих парабол имеют отрицательное направление, определяемое вектором .

Date: 2015-12-10; view: 406; Нарушение авторских прав