Различные способы задания прямой в пространстве

Пусть 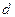- прямая в пространстве, точка - некоторая точка этой прямой. Напомним, что любой ненулевой вектор , параллельный этой прямой, называется ее направляющим вектором.

Ясно, что прямая имеет бесконечное множество направляющих векторов, любые два из которых коллинеарны.

Тогда векторы и коллинеарны:

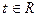= , где (1)

Таким образом, чтобы задать прямую 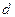, достаточно задать ее точку и направляющий вектор , при этом пишем = .

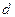Формула (1) устанавливает взаимно однозначное соответствие между точками прямой 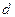и значениями параметра .

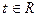Возьмем какую-либо аффинную систему координат в пространстве (рис.26), и пусть относительно нее точки и 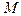имеют координаты 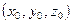, . Вектор разложим по векторам базиса 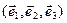: . Тогда координатная запись равенства (1) имеет вид:

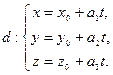(2)

Таким образом, уравнения (2) определяют прямую в пространстве. Они называются параметрическими уравнениями прямой.

Если , то исключая из уравнений (2), плучим . (3)

Если одна из координат направляющего вектора 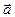прямой равна нулю, например, , то

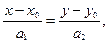
(3) . (3^/)

В этом случае прямая параллельна плоскости , .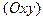

Если две координаты направляющего вектора 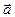прямой равны нулю, например, , то и

(3) ,

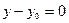В этом случае прямая , в частности .

Уравнения (3), 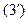, называются каноническими уравнениями прямой.

Прямая будет определена, если задать две её различные точк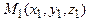и и 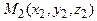.При этом вектор с координатами служит направляющим вектором этой прямой. Также в этом случае уравнения прямой можно записать в виде (2) и (3):

, .

Прямая может быть задана как линия пересечения двух плоскостей , т.е. (4)

где – условие пересечения плоскостей и . Параметрические уравнения прямой получены в § 23 и имеют вид:

, , . (5)

Заметим, что в прямоугольной системе координат направляющий вектор 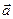прямой может быть найден как векторное произведение , где 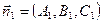– векторы нормалей плоскостей и соответственно.

§28. Взаимное расположение двух прямых, прямой и плоскости

1. Взаимное расположение прямой и плоскости.

Относительно системы координат заданы прямая d системой (1)

и плоскость П общим уравнением:

. (2)

Для того, чтобы выяснить их взаимное расположение, будем искать общие точки прямой d и плоскости П. Для этого нужно решить систему уравнений (1) и (2). Заменяя х, у, z в уравнении (2) по формулам (1), получим уравнение относительно параметра t:

(3)

Здесь возможны случаи:

1. система уравнений (1), (2) имеет единственное решение. Таким образом, это условие является необходимым и достаточным условием пересечения прямой d и плоскости П.

2. , .

В этом случае уравнение (3) не имеет решений, а значит и система (1),(2) не имеет решения, т.е. прямая и плоскость параллельны.

3.

В этом случае уравнение (3) удовлетворяется любым значением t, а значит система (1), (2) имеет бесконечное множество решений. Следовательно, каждая точка прямой d принадлежит плоскости II, т.е.прямая лежит на плоскости.

2. Взаимное расположение двух прямых в пространстве

Пусть имеем две прямые , , каждая из которых задана точкой и направляющим вектором с координатами (рис.27):, относительно аффинной системы координат .Обозначим

, ,

1) Векторы - некомпланарны detA ¹ 0. Следовательно, прямые и скрещиваются.

2) Векторы 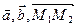- компланарны det À = 0. Следовательно, прямые и лежат в одной плоскости.

а) векторы - неколлинеарны rangB = 2. Тогда прямые и пересекаются.

б) векторы и - коллинеарны, и - неколлинеарны rangB = 1, rangC = 2. При этом прямые и параллельны.

3) Векторы 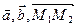коллинеарны rangB = 1, rangC = 1 rangА = 1. Следовательно, прямые и совпадают.

Date: 2015-12-10; view: 1976; Нарушение авторских прав