Поверхности второго порядка. 1. Уравнением поверхности в некоторой системе координат в пространстве называется уравнение

1. Уравнением поверхности в некоторой системе координат в пространстве называется уравнение

, (1)

которому удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты ни одной точки, не принадлежащей поверхности.

Все поверхности подразделяются на два больших класса: алгебраические и неалгебраические и могут быть изучены методом сечений: рассматривают сечения поверхности плоскостями, параллельными координатным плоскостям; по виду этих сечений определяют свойства и форму этой поверхности.

Поверхность F называется алгебраической, если в какой-нибудь аффинной системе координат ее уравнение можно записать в виде (1), в котором - многочлен относительно .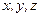

Порядком алгебраической поверхности называется степень ее уравнения в какой-либо системе координат (то есть степень многочлена 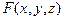в уравнении (1) этой поверхности).

Все поверхности первого порядка являются плоскостями. Сфера является примером поверхности второго порядка.

1 .Цилиндрические поверхности второго порядка.

Поверхность, обладающая тем свойством, что вместе с каждой своей точкой М она содержит всю прямую, проходящую через эту точку, параллельно данному ненулевому вектору 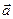, называется цилиндрической поверхностью или цилиндром.

Прямые, параллельные вектору 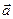и принадлежащие цилиндрической поверхности, называются образующими этой поверхности.

Цилиндрическая поверхность F может быть образована следующим образом. Пусть g - некоторая линия, а 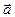- ненулевой вектор. Множество всех точек 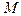пространства, принадлежащих тем параллельным прямым с направляющим вектором 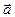, которые пересекают линию g, образуют цилиндрическую поверхность. Линия g называется направляющей этой поверхности.

Если прямоугольную систему координат выбрать так, чтобы образующие цилиндрической поверхности были параллельны вектору , а направляющая линия 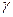в репере 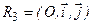имела каноническое уравнение второго порядка, то цилиндрические поверхности второго порядка определяются следующими уравнениями:

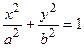-эллиптический цилиндр;

- гиперболический цилиндр;

-параболический цилиндр;

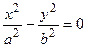- цилиндр, распавшийся на пару пересекающихся по оси (Oz) плоскостей;

- цилиндр, распавшийся на пару параллельных плоскостей;

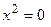- пара слившихся плоскостей.

Эти уравнения называются каноническими уравнениями цилиндрических поверхностей второго порядка.

Date: 2015-12-10; view: 593; Нарушение авторских прав