
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общее уравнение плоскости в задачах
|
|
1. Напомним, что вектор 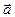 параллелен плоскости
параллелен плоскости 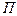
 , если
, если  .
.
Лемма. Пусть в аффинной системе координат  заданы плоскость
заданы плоскость 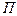 уравнением
уравнением
 ,
,  )
)
и вектор  . Для того чтобы вектор
. Для того чтобы вектор  был параллелен плоскости
был параллелен плоскости 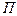 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
 . (1)
. (1)
Доказательство. От некоторой точки  плоскости
плоскости 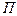 отложим вектор
отложим вектор  и обозначим через
и обозначим через  координаты точки
координаты точки  . Тогда
. Тогда


 (2)
(2)
Так как  , то
, то  . (3)
. (3)
Пусть вектор  параллелен плоскости
параллелен плоскости 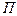 . Тогда точка
. Тогда точка  лежит в этой плоскости, поэтому
лежит в этой плоскости, поэтому
 . (4)
. (4)
Из равенств (3) и (4) следует, что
 (5)
(5)
или, учитывая равенства (2), получим равенство (1).
Обратно, пусть выполняется равенство (1). Подставив сюда значения  из равенства (2), получим равенство (5). Сложив равенства (3) и (5), приходим к равенству (4). Таким образом,
из равенства (2), получим равенство (5). Сложив равенства (3) и (5), приходим к равенству (4). Таким образом,  , то есть вектор
, то есть вектор  параллелен плоскости
параллелен плоскости 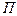 .
.
2. Полупространство.
Пусть в аффинной системе координат  задана плоскость
задана плоскость 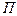 уравнением
уравнением
 ,
,  )
)
 Плоскость
Плоскость 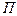 разделяет множество не принадлежащих ей точек пространства на две части, каждая из которых вместе плоскостью П образует полупространство, ограниченное этой плоскостью. Пусть
разделяет множество не принадлежащих ей точек пространства на две части, каждая из которых вместе плоскостью П образует полупространство, ограниченное этой плоскостью. Пусть 
 Так как
Так как  , то вектор
, то вектор 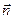 не параллелен плоскости П и
не параллелен плоскости П и  и, следовательно, точка
и, следовательно, точка  принадлежит только одному из указанных полупространств.
принадлежит только одному из указанных полупространств.
Через точку  проведем прямую параллельно прямой
проведем прямую параллельно прямой  и обозначим через
и обозначим через  точку пересечения этой прямой с плоскостью П. Так как векторы
точку пересечения этой прямой с плоскостью П. Так как векторы 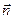 и
и  коллинеарны, то существует такое число
коллинеарны, то существует такое число 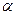 , что
, что  , или в координатах:
, или в координатах:
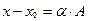 ,
,  ,
, 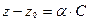 (6)
(6)
Векторы  и
и  одинаково направлены (точки
одинаково направлены (точки 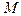 и
и  - в одном полупространстве, ограниченном плоскостью П) тогда и только тогда, когда
- в одном полупространстве, ограниченном плоскостью П) тогда и только тогда, когда  . Эти векторы противоположно направлены (точки
. Эти векторы противоположно направлены (точки 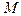 и
и  - в разных полупространствах, ограниченных плоскостью П) тогда и только тогда, когда
- в разных полупространствах, ограниченных плоскостью П) тогда и только тогда, когда  .
.
Тогда, учитывая (6), имеем:



 , так как
, так как  .
.
Так как  , то знак
, то знак  совпадает со знаком
совпадает со знаком 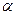 . Следовательно,
. Следовательно, 
 , где
, где 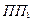 – полупространство, ограниченное плоскостью П и содержащее точку
– полупространство, ограниченное плоскостью П и содержащее точку 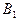 , и
, и 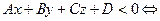
 , где
, где  – полупространство, ограниченное плоскостью П и не содержащее точку
– полупространство, ограниченное плоскостью П и не содержащее точку 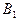 .
.
3. Расстояние от точки до плоскости.
 В прямоугольной системе координат
В прямоугольной системе координат  дана плоскость
дана плоскость  :
:  =0 и точка
=0 и точка  , не лежащая в этой плоскости (рис.25). Определим расстояние
, не лежащая в этой плоскости (рис.25). Определим расстояние  от точки до плоскости
от точки до плоскости  . Пусть
. Пусть  - основание перпендикуляра, проведенного из точки
- основание перпендикуляра, проведенного из точки  к плоскости
к плоскости  . Вектор
. Вектор 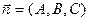 перпендикулярен плоскости
перпендикулярен плоскости  и, следовательно, коллинеарен вектору
и, следовательно, коллинеарен вектору  .
.
Используя скалярное произведение, находим искомое расстояние:
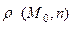 =
= 

 . Учитывая, что
. Учитывая, что  , т.е.
, т.е.  , получаем
, получаем
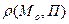 =
=  . (7)
. (7)
Date: 2015-12-10; view: 365; Нарушение авторских прав