Ранг матрицы. Рассмотрим матрицу А размерности :

Рассмотрим матрицу А размерности :

Обозначим строки матрицы А соответственно: .

Говорят, что строка является линейной комбинацией строк если , (1)

где - действительные числа.

Строку называют нулевой, обозначают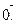

Система строк линейно зависима, если существуют числа , не равные нулю одновременно, что имеет место . В противном случае система – линейно независима.

Рассмотрим некоторые свойства системы линейно зависимых строк.

1. Система , (2)

содержащая нуль вектор 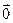, линейно зависима.

Утверждение очевидно, т.к.

, где

2. Система , линейно зависима тогда и только тогда, когда хотя бы одна из них является линейной комбинацией остальных строк этой системы.

Действительно, если система линейно зависима, то в равенстве , отлично от нуля по крайней мере одно из чисел допустим для определенности 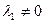, то .

Значит, строка есть линейная комбинация остальных.

Обратно: пусть , то ; т.к. , то система (2) линейно зависима.

3. Если часть системы (подсистема) линейно зависима, то и вся система (2) линейно зависима.

Пусть система - линейно зависимая подсистема системы 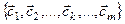, тогда существуют числа , не равные нулю одновременно, такие, что . Это равенство можно записать так:

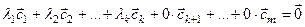, откуда очевидно, что и вся система (2) линейно зависима.

4. Если система (2) линейно независима, то любая ее подсистема линейно независима.

Утверждение очевидно: предположив противное, в силу свойства 3 получим противоречие условию 4.

Максимальное число линейно независимых строк матрицы называется (строчечным) рангом матрицы, пишут rang A (или rank A).

Для нахождения (строчечного, столбцового) ранга матрицы применяют следующие элементарные преобразования:

- вычеркивание нулевой строки (столбца),

- прибавление к одной из строк (одному из столбцов) другой строки (столбца), умноженной на любое число,

- умножение строки (столбца) на число, отличное от нуля,

- перестановка столбцов (строк).

В силу перечисленных свойств 1-4 очевидно, что элементарные преобразования не меняют ранг матрицы. Присоединение к матрице строки, полученной линейной комбинацией строк, не меняет ранг матрицы.

Теорема1. Матрица треугольного вида А = имеет ранг, равный количеству элементов на главной диагонали.

Доказательство. Обозначим строки этой матрицы: . Тогда

Система равносильна условию: Таким образом, rang А= k.

Теорема2. Максимальное количество линейно независимых строк матрицы равно максимальному количеству линейно-независимых столбцов матрицы, т.е. строчечный ранг матрицы равен её столбцовому рангу и называется рангом матрицы.

Доказательство теоремы опирается на то, что при помощи элементарных преобразований строк и столбцов любую матрицу можно привести к матрице диагонального вида. Тогда утверждение очевидно в силу теоремы 1.

Пример. Вычислить ранг матрицы:

В =

Решение: приведем матрицу В с помощью элементарных преобразований к треугольному виду.

~ ~

~ ~ .

Значит, ранг матрицы В равен 4.

Date: 2015-12-10; view: 387; Нарушение авторских прав