
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. а) По формуле (3.28) длина вектора векторного произведения:
|
|
а) По формуле (3.28) длина вектора векторного произведения: 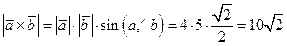 .
.
б) По свойствам векторного произведения найдем
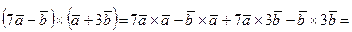

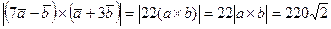 .
.
Пример 2. Заданы векторы  и
и  . Найти координаты векторов а)
. Найти координаты векторов а) 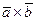 ; б)
; б)  .
.
Решение. а) Используем формулу (3.31) вычисления координат вектора векторного произведения векторов  и
и 
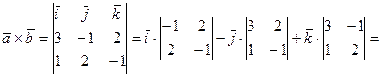

б) Сначала определим координаты векторов
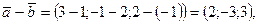
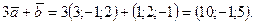 Снова используем (3.31)
Снова используем (3.31)
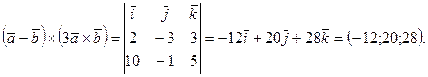
Пример 3. Определить единичный вектор  , перпендикулярный каждому из векторов
, перпендикулярный каждому из векторов  ,
,  , образующий острый угол с осью
, образующий острый угол с осью 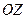 .
.
Решение. Найдем координаты вектора
 . По определению векторного произведения векторов
. По определению векторного произведения векторов 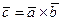 перпендикулярен и
перпендикулярен и  , и
, и 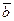 . Значит
. Значит  . Найдем орт вектора
. Найдем орт вектора 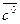 :
:

Тогда 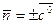 . Выбираем знак +, т.к. в этом случае третья координата вектора положительна, значит, вектор образует острый угол с осью
. Выбираем знак +, т.к. в этом случае третья координата вектора положительна, значит, вектор образует острый угол с осью 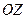 . Значит
. Значит  .
.
Пример 4. Найти площадь параллелограмма, построенного на векторах 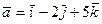 и
и  .
.
Решение. Согласно формуле (3.32) 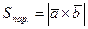 . Учитывая координатный способ задания векторов, найдем сначала координаты вектора
. Учитывая координатный способ задания векторов, найдем сначала координаты вектора
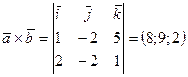 .
.
А теперь его модуль
 .
.  .
.
Пример 5. В треугольнике с вершинами 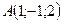 ,
,  ,
,  найти длину высоту, опущенной из вершины
найти длину высоту, опущенной из вершины  на сторону
на сторону  .
.
Решение. Обозначим 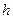 длину высоты из вершины
длину высоты из вершины  , тогда
, тогда 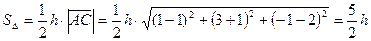 .
.
С другой стороны 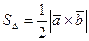 , где
, где  ,
,  . Определим
. Определим 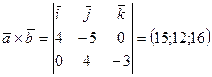 ,
,  .
.
Итак, 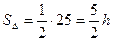 . Откуда
. Откуда 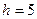 .
.
Пример 8. Найти координаты вектора  , если известно, что он перпендикулярен векторам
, если известно, что он перпендикулярен векторам  и
и  , образует с ортом
, образует с ортом 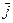 тупой угол и
тупой угол и 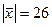 .
.
Решение. По условию  и
и 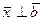 , следовательно
, следовательно  . Найдем
. Найдем
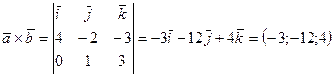 .
.
По условию коллинеарности векторов 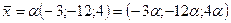 . Найдем
. Найдем  из условия
из условия 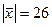 .
.
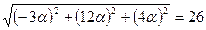 ,
,  ,
,  ,
,
 . Если
. Если  , то
, то 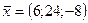 . Проекция на ось OY равна
. Проекция на ось OY равна 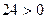 , этот вектор образует с
, этот вектор образует с 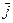 острый угол. При
острый угол. При 
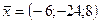 образует тупой угол с вектором
образует тупой угол с вектором 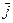 , что удовлетворяет условию.
, что удовлетворяет условию.
Date: 2015-12-10; view: 477; Нарушение авторских прав