Действия над векторами, заданными своими координатами. Пример 1.Найти координаты орта вектора

Пример 1. Найти координаты орта вектора .

Решение. По формуле (1.1) вектор может быть представлен в виде произведения модуля вектора на орт этого вектора, то есть .

Найдем по формуле (2.4) .

Значит .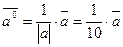

Выполняя умножение вектора на число получим: .

Пример 2. Даны два вектора и . Найти и .

Решение. Векторы и 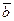заданы в виде разложения по базису 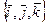. Коэффициенты этих разложения являются прямоугольными координатами векторов, значит и 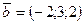. По правилам действий над векторами в координатной форме находим , и . Теперь находим длины этих векторов по формуле (3.8)

, ,

,

.

Пример 3. Найти длину и направляющие косинусы медианы треугольника , если , , .

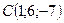Решение. Найдем координаты точки середины отрезка по формуле (3.18)

, , .

Значит 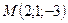. Определим координаты вектора .

Длина медианы или модуль вектора определим по формуле (3.9)

.

Направляющие косинусы вектора определим с использованием формул (3.10)

, , .

Пример 4. Даны три вектора . Вектор разложить по векторам .

Решение. Разложить вектор по векторам - это значит, представить его в виде линейной комбинации этих векторов, т.е.

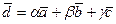, где 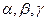- некоторые числа.

Перейдем в этом векторном равенстве к координатам

или

.

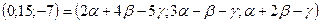Учитывая условие равенства векторов, получим систему:

решение которой т.е. .

Date: 2015-12-10; view: 830; Нарушение авторских прав