Типы мышления, их классификация, характеристики

Остается составить таблицу всех вариантов, а точнее, типов мышления, которые для удобства мы будем именовать следующим образом:

• тип «точка и мнимые прямые» – это «разрушитель», «мечтатель»;

• тип «точка и действительные прямые» – это «революционер» (обновляющий);

• параболический тип мышления – это «ищущий новое»;

• эллиптический тип мышления – это «создающий свой мир»;

• гиперболический тип мышления – это «копирующий» готовые модели;

• тип «параллельные прямые» – это «наводящий порядок» в мире.

Таблица 1. Определение типов мышления

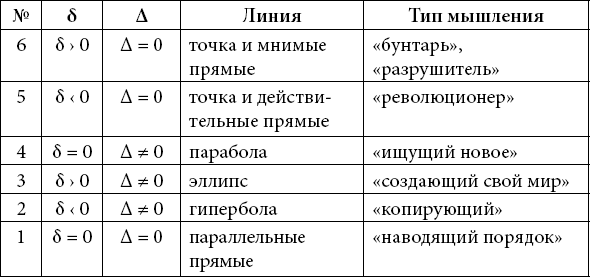
Одного взгляда на таблицу достаточно, чтобы понять – мы можем определить каждый тип, для этого достаточно иметь матрицу и значения определителей.

Таблица 2. Качества людей в соответствии с типом мышления

Как вы сами можете видеть, теперь нам достаточно выполнить расчеты определителей по конкретной матрице, и мы получим представление о типе мышления конкретного ребенка или взрослого человека.

Однако мы до сих пор не знаем, где и как нам заполучить матрицу, которая была бы связана с конкретным человеком или ребенком. Что ж, научимся рассчитывать нужные нам матрицы, опираясь на дату рождения человека и на методы цифрового анализа.

Нам потребуется конкретная дата рождения, на примере которой мы могли бы провести полное исследование по определению типа мышления конкретного новорожденного. Предлагаю рассмотреть дату рождения красавицы, от судьбы которой зависит жизнь миллиардов людей.

Знакомьтесь, Россия Эсэсэровна Многострадальная, день рождения: 12 июня 1990 года.

Приступим к расчету матрицы.

1. Запишем дату:

12 6 1990

2. Выполним расчет дополнительных чисел:

Первое число: 1+2+6+1+9+9+0=28

Второе число: 2+8=10

Третье число: 28–1·2=28–2=26

Четвертое число: 2+6=8

Итог: 12 6 1990

28 10 26 8

3. Запишем психоматрицу:

запишем цифровую матрицу:

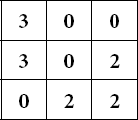
4. Выполним расчет определителей.

Запишем формулы расчета обоих определителей в общем виде:

Имеется матрица 3×3, тогда:

δ = am – kb;

Δ = (amr + bno + kcp) – (omc + kbr + anp)

Выпишем малую матрицу:

Рассчитаем малый определитель по формуле:

δ = am – kb,

δ = 30–3•0 = 0–0 = 0;

Итог: δ = 0.

Рассчитаем большой определитель по формуле:

Δ = (amr + bno + kcp) – (omc + kbr + anp),

Δ = (30•2 + 0•2•0 + 3•2•0) – (0•0•0 + 3•0•2 + 3•2•2) = (0 + 0 + 0) – (0 + 0 + 12) = – 12 ≠ 0;

Итог: Δ ≠ 0.

Общий итог: δ = 0, Δ ≠ 0.

Линия: парабола.

Тип мышления: «ищущий новое».

Дополнительная информация: Исследователь, теоретик, философ, мыслитель, способный интуитивно выделять неизвестные на данный момент объекты (темы исследований), которые в ближайшем или далеком будущем будут весьма важны и перспективны; он способен выделить отдельные важные параметры нового объекта, определить направление исследования и составить прогноз на возможные результаты исследования.

Согласитесь, утешительный результат. Можно уверенно сказать, что мы живем в обновляющейся и строящейся стране. Особенно радует, что строители новой России пытаются предвидеть ее возможное будущее, заглядывают в близкую и далекую перспективу, пытаясь найти наиболее оптимальные важнейшие вехи, которые указали бы конечную цель преобразований и реформ, которым не может быть предела. Важен сам процесс поиска нового, вечного поиска нового.

[1]Асимптотой называется прямая, к которой линия стремится приблизиться, но никогда ее не достигает (не касается).

Date: 2015-10-21; view: 1461; Нарушение авторских прав