Динамических нагрузок горных машин

Важнейшими параметрами случайных процессов являются математическое ожидание М_x, дисперсия D_x, среднеквадратичное значение s_x, функция распределения вероятности (F_x), корреляционная функция K_x (t) и спектральная плотность мощности S_x (t). Две последние характеристики являются наиболее полными, содержащими информацию, как о частотном составе, так и о распределении энергии вибрационного процесса.

Для статистического анализа динамических нагрузок горных машин используем теорию случайных стационарных процессов, хотя в действительности режим работы машины не является стационарным в строгом определении этого понятия. Однако при испытаниях почти всегда можно выбрать временные участки процесса, на которых это условие с достаточной на практике точностью выполняется. Рассмотрим теоретические предпосылки выбора необходимых статистических параметров случайной вибрации горной машины.

В основу теории статистического анализа случайных стационарных процессов положена теорема Винера-Хинчина [6], представляющая пару взаимных преобразований Фурье корреляционной функции K_x (t) и спектральной плотности мощности S_x (t):

, (2.1)

где

(2.2)

- спектральная плотность мощности в диапазоне частот ω.

Полагая в формуле (2.1) корреляционный сдвиг t = 0 и, проинтегрировав в интервале положительных частот, имеющих физический смысл, получаем выражение интегральной спектральной функции, которая выражает полную мощность процесса в полосе частот dw от 0 до ∞:

. (2.3)

В этой формуле выражение под знаком интеграла представляет собой не что иное, как дисперсию процесса, извлекая из которой корень квадратный, получим среднеквадратичное значение случайной функции в диапазоне частот dω от 0 до ∞:

. (2.4)

Функция S(ω) выражает мощность процесса колебаний, приходящуюся на интервал частот dω и является непрерывной. Мощность процесса, заключенную в конечной полосе частот Δ ω, определяет значение интегральной функции . Среднеквадратичное значение s_x также пропорционально мощности процесса в интервале частот dω. Однако в отличие от S(ω) и , прямо пропорциональных мощности, s_x имеет степенную зависимость.

Наши практические рекомендации, опубликованные в работе [8] для определения статистически достоверного параметра s_x заключаются в следующем. Основой большинства экспериментальных способов получения спектральной плотности мощности является уравнение:

, (2.5)

где P(f) – спектральная плотность мощности;

В – ширина полосы частотного пропускания фильтра анализатора Δ f=f₂–f₁, Гц;

Т – время усреднения, с;

x(f,t) – функция абсолютных значений случайной величины.

Для экспериментального измерения спектральной плотности требуется сравнительно сложная и дорогостоящая аппаратура, выпускаемая зарубежными фирмами, которую исследователи не всегда имеют возможность применить. В этой связи для частотного анализа колебаний часто используются среднеквадратичные спектры, экспериментальное получение которых сравнительно не сложно в техническом плане.

Из формулы (2.5) видно, что выражение под знаком интеграла представляет собой квадрат эффективного (среднеквадратического) значения случайной функции. Следовательно, среднеквадратичные спектры содержат информацию о пропорциях распределения энергии случайного процесса в полосах частотного пропускания фильтра анализатора. Если правильно учитывать возникающие погрешности при аппаратурном анализе, такие спектры дают сравнительно представительную статистическую картину случайных колебаний. При аппаратурном анализе каждый из элементов измерительного тракта (виброизмерительный преобразователь – акселерометр, предварительный усилитель, усилитель, частотный фильтр, регистрирующий прибор – стрелочный или самопишущий) вносят отдельные погрешности, которые необходимо учитывать. Кроме того, необходимо учитывать погрешность калибровки измерительного тракта, а также статистические погрешности. Если не учитывать статистические погрешности, то это может привести к значительным ошибкам измерения случайного сигнала.

Формула для расчета относительной статистической погрешности при измерении эффективного значения случайной величины имеет вид:

, (2.6)

Из формулы (2.6) видно, что для уменьшения величины статистической погрешности при заданной ширине В полосы пропускания фильтра анализатора необходимо максимальное увеличение времени усреднения Т. На практике длительность времени усреднения ограничивается разумными пределами продолжительности времени аппаратурного анализа.

Для минимизации времени усреднения при величине суммарной погрешности в пределах допустимых значений нами предложена следующая методика:

- исследователь задается величиной суммарной допустимой погрешности измерения, она не должна превышать

25-30%, что при анализе случайных сигналов считается

хорошим результатом. Или в относительных к 100% значениях e_сд £ 25-30/100£ 0,25-0,3;

- погрешности частотных характеристик отдельных элементов измерительного тракта ε_i рассматриваются как частные случайные величины, в этом случае суммарную погрешность можно выразить следующей зависимостью

, (2.7)

где ε_к – погрешность калибровки;

- подставляем в формулу (2.7) выражение статистической погрешности измерения (2.6) и, решив полученное уравнение, относительно времени усреднения, запишем зависимость для расчетов требуемого времени усреднения

. (2.8)

При расчетах времени усреднения по формуле (2.8) погрешности подставляются в относительных к 100% величинах. Определенное таким образом время усреднения приводится в соответствие со скоростью пера самописца уровня вибрации или с «демпфированием» стрелки на показывающем приборе (Т, которое может быть равно: 0,1с; 0,5с; 1с; 5с; 10с и т.п.).

Однако при исследовании колебаний и разработке средств снижения динамических нагрузок горных машин спектральная плотность мощности процесса представляет более полную информацию о распределении энергии колебаний в отдельных полосах частот. Рассмотрим варианты её получения по экспериментальным данным и связанные с этим погрешности.

Определение экспериментальной спектральной плотности по методу корреляционной функции на основе формулы (2.2) с использованием специальных приборов-корреляторов механических, фотоэлектрических, магнитных, чрезвычайно громоздко и сложно с точки зрения технической реализации аппаратурной системы.

Интенсивное развитие вычислительной техники за последнее время открыло широкие возможности цифровой обработки временных характеристик записей колебаний (например, на магнитограф для записи преобразованных в электрический сигнал колебаний) с последующими вычислениями на ЭВМ статистических параметров: математического ожидания М_x, дисперсии D_x, среднеквадратичного значения s_x, функции распределения вероятности (F_x), корреляционной функции K_x (t) и спектральной плотности мощности S_x (t).

Рассмотрим возможные погрешности, возникающие при таких вычислениях. Полагая в формуле (2.2) ω = 2πf, перепишем её в виде

, (2.9)

где представлены теоретические интервалы -¥ < t < +¥; -¥ < ¦ < +¥.

Обозначим: и

На практике теоретическая формула (2.9) изменяется. Интегрирование в бесконечных пределах заменяют интегрированием на конечном отрезке корреляционной функции 0 - t_m, а в место используют оценку - K_x (t). Кроме того, для и учитывают только положительные значения аргументов функций и так как они четные. В результате исходная формула (2.9) приобретает следующий вид:

, (2.10)

где G_x(f) – оценка спектральной плотности процесса.

Выражение (2.9) записывается в другом виде, учитывая, что корреляционная функция задана на конечном отрезке своего аргумента:

. (2.11)

Здесь введена функция временного или корреляционного «окна»

равная:

(2.12)

Применив к выражению (2.11) теорему о свертке двух функций, получим

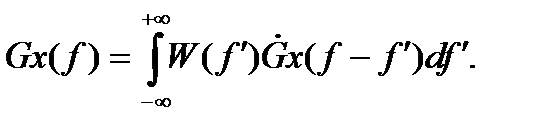
Подынтегральные функции в этом выражении есть преобразования Фурье от функций h(t) и K_x(t) соответственно. Таким образом, из-за того, что корреляционная функция подсчитывается на конечном отрезке своего аргумента, получаемая на практике спектральная плотность, является результатом усреднения теоретического значения с помощью некоторой весовой функции W(f), называемой функцией спектрального окна.

Функция корреляционного окна h(t) является четной функцией, поэтому преобразование Фурье от h(t) есть действительная функция:

То же самое относится к корреляционной функции и её преобразованию Фурье:

В данном случае «спектральное окно» является характеристикой эквивалентного анализирующего фильтра, а – теоретической спектральной плотностью.

Эта аналогия с фильтровым методом анализа показывает, что с одной стороны, вычисленное значение в заданной точке является усредненной величиной на интервале полосы пропускания «спектрального окна». А с другой стороны, получаемая оценка является состоятельной, также как и при фильтровом методе анализа. Рассмотрим подробнее функцию h(t) и соответствующую ей функцию W(f).

Корреляционное окно h(t), заданное выражением (2.12) может иметь форму прямоугольного окна (см. рис. 2.1 а). Преобразование Фурье этой функции равно:

Из рис.2, а видно, что по бокам основного пика функции W(f) имеются дополнительные положительные и отрицательные всплески.

Рис.2.1. Корреляционные и спектральные окна

Очевидно, что анализирующий фильтр с подобной характеристикой является не подходящим с физической точки зрения. При его использовании график G_x(f) будет содержать ложные пики и не имеющие физического смысла отрицательные выбросы.

Ввиду явных недостатков функции прямоугольного корреляционного окна были предложены некоторые другие функции, например, «Окно Бартлета», рис. 2.1, б,котороезадают следующим образом:

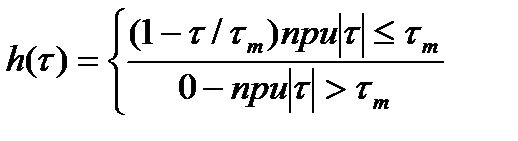(2.13)

В частотной области эта функция не имеет отрицательных выбросов, но боковые всплески присутствуют, хотя они менше, чем в предыдущем случае. Попутно следует отметить, что применение “окна Бартлета” равносильно определению G_x(f) путем усреднения G_x1(f)…G_xi(f), полученных для равных отрезков, на которые разбита исходная реализация длиной Т.

Окно Хеннинга, рис. 2.1, в:

(2.14)

Окно Хемминга, рис. 2.1, г:

(2.15)

Окно Хемминга, рис.2.1, г, обладает наименьшими боковыми всплесками из всех рассмотренных. В литературе описаны и некоторые другие функции h(t), использованные для целей спектрального анализа. Практический опыт показывает, что все известные функции корреляционного окна, за исключением «прямоугольного окна», дают почти одинаковые результаты. Флуктуации спектра, вызванные наличием боковых всплесков на «спектральном окне», обычно не превышают погрешностей анализа. Однако если выбор того или иного корреляционного окна не лимитируется какими-либо причинами, то имеет смысл использовать «окно Хемминга».

Для определения статистической погрешности спектрального анализа необходимо определить эффективную полосу пропускания спектрального окна Δ f_э, т.е. ширину полосы пропускания фильтра с прямоугольной характеристикой, при использовании которого дисперсия оценки G_x(f) получается такая же, как и при заданном спектральном окне.

Для описанных выше функций h(t) расчеты дают следующие значения Δ f_э:

(2.16)

Анализ зависимостей (2.16) показывает, что эффективная полоса частот спектрального окна, обратно пропорциональна длине отрезка корреляционной функции, который используется при вычислении G_x(f). Это означает, что чем длиннее корреляционная функция, которая используется для определения G_x(f), тем лучним разрешение по частоте подсчитывается спектральная плотность. Можно также заметить, что при одинаковой величине Δ f_э из всех практически целесообразных функций h(t) функция «окна Хемминга» требует наименьшей величины t_m. Это следует учитывать, так как основная трудоемкость определения спектральной плотности состоит в вычислении корреляционной функции.

При проведении спектрального анализа выбор величины Δ f_э считается важным отправным моментом. От величины Δ f_э зависит статистическая погрешность анализа и его разрешающая способность. Требования увеличения разрешающей способности и уменьшения статистической ошибки противоречивы. В данном случае возникает такая же проблема, как и при фильтровом методе анализа. Решение этого вопроса зависит от физической сущности исследуемых процессов и целей спектрального анализа. Если рассматривать обычные колебательные процессы, протекающие, например, в подвесках автомобилей, то среди основных и существенных деталей спектров их колебаний наиболее узкополосные «пики» сосредоточены в низкочастотной зоне. Однако в тех случаях, когда требуется максимальная разрешающая способность анализа во всем диапазоне частот, нужно сохранять постоянную ширину «спектрального окна».

После того, как эффективная ширина полосы пропускания спектрального окна - Δ f_э определена подсчет статистической погрешности не представляет труда. Для этого необходимо подставить величину D f_э в формулу для расчета дисперсии полученной оценки:

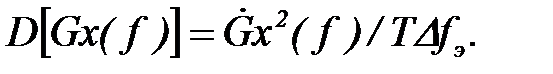(2.17)

Относительная дисперсия ошибки

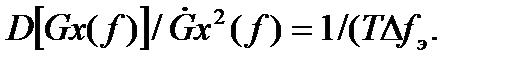(2.18)

При определении доверительных интервалов с помощью формул (2.17) и (2.18) следует учитывать, что закон распределения случайной величины G_x(f) может считаться нормальным лишь при Больших длительностях реализации и широкой полосе частот Δ f_э. Фактически этот закон описывается c -распределением. Параметр c -распределения - n (число степеней свободы) равно [7]:

(2.19)

Нормальный закон распределения для оценки G_x(f) может быть принят только при n > 100. На практике n = 30-90, потому для построения доверительных границ лучше пользоваться таблицами c -распределения или графиками для определения верхней и нижней доверительных границ G_x(f) в зависимости от величины n.

Таким образом, для исследования статистических параметров вибрации горных машин, во-первых, целесообразно принимать корреляционное «окно Хэмминга». Во-вторых, при исследовании вибрации горной машины и в частности карьерных экскаваторов, ставится задача выбора величины эффективной полосы частот спектрального окна - Δ f_э, от величины которой зависит статистическая погрешность анализа и его разрешающая способность, достаточная для частотной детализации вибрационного процесса. В-третьих, ставится задача обоснованного выбора длительности реализации Т, позволяющей получить достаточное число точек цифрового массива для достоверного спектрального анализа динамических нагрузок горной машины. В-четвертых, к обоснованию принятых для дальнейших исследований значений D f_э и Т необходимо выполнить вычисление показателей статистической надежности: числа степеней свободы - n; дисперсии ошибки - D_o; среднеквадратичного отклонения – s_D; относительной доверительной вероятности - a и относительного доверительного интервала - x.