Понятие производственной функции и функции издержек производства

Модели экономического равновесия

Понятие производственной функции и функции издержек производства

В реальной жизни в пределах используемой технологии предприниматель стремится найти наилучшее сочетание факторов производства, чтобы достичь наибольшего выхода продукции. Отношение между любым набором факторов производства и максимально возможным объемом продукции, производимой из этого набора факторов, характеризует производственную функцию.

Производственная функция отражает зависимость объема выпуска продукции от затрат ресурсов (факторов) производства.

(4.1.1)

где, q – объем выпуска продукции;

ТС – издержки производства.

В микроэкономике используется большое количество самых разнообразных функций производства, но чаще всего — двухфакторные функции вида: . Среди двухфакторынх функций наибольшую известность получила функция Кобба-Дугласа, имеющая вид:

(4.1.1)

где, a, b, c – коэффициенты функции;

K, L – количество используемых ресурсов (капитал и труд).

Функция издержек производства – это зависимость полных затрат от объема выпускаемой продукции.

(4.1.2)

где, с – затраты на ед. производимой продукции.

Издержки производства продукции можно разделить на условно-постоянные FC (которые не изменяются при изменении объеме производства в пределах существующей мощности) и переменные VC (которые изменяются при изменении объеме производства).

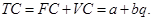
(4.1.2)

Цена единицы р продукции формируется на рынке и зависит от соотношения спроса и предложения. Представим функцию зависимости цены от объема продукции.

(4.1.3)

где, Q – это объем предложения продукции на рынке.

Доход фирмы TR, получаемый от реализации продукции, равен произведению цены продукции р на объем производства фирмы.

(4.1.4)

Прибыль фирмы p представляет собой разницу между доходом и издержками производства.

(4.1.5)

Введем понятия: совокупный, средний и предельный продукт, издержки и доход.

Совокупный продукт (TQ) — общий объем произведенной фирмой продукции за единицу времени.

Средний продукт (AQ) — это объем выпуска продукции на единицу затрат.

(4.1.5)

Предельный продукт (MQ) — величина прироста совокупного продукта, при изменении затрат на одну единицу, т.е. это производная от производственной функции.

(4.1.5)

Совокупные издержки (TC) — общие издержки на производства продукции.

Средние издержки (AС) — это издержки на единицу выпускаемой продукции.

(4.1.5)

Средние переменные издержки (AVС) — это переменные издержки на единицу выпускаемой продукции.

(4.1.5)

Средние постоянные издержки (AFС) — это постоянные издержки на единицу выпускаемой продукции.

(4.1.5)

Предельные издержки (MС) — величина прироста издержек при изменении объема выпускаемой продукции на одну единицу, т.е. это производная от функции издержек.

(4.1.5)

Так как постоянные издержки не меняются с изменением объема выпускаемой продукции, предельные издержки определяются ростом лишь переменных издержек в результате выпуска дополнительной единицы продукции.

Совокупный доход (TR) – это совокупная денежная сумма, полученная от продажи определенного количества товара.

Средний доход (AR) – это выручка от реализации единицы продукции, т.е. валовой доход, приходящийся на единицу проданной продукции.

(4.1.5)

Предельный доход (MR) — величина прироста дохода при изменении объема выпускаемой продукции на одну единицу, т.е. это производная от функции дохода.

(4.1.5)

Date: 2015-10-19; view: 896; Нарушение авторских прав