Общие классы моделей

Модель, отражающая однозначное соответствие реальной системе в области функций или структуры, называется изоморфной. При по­строении моделей сложных систем практически не удается достигнуть полного изоморфизма, за исключением моделей клонирования и, час­тично, искусственного интеллекта, поэтому исследуемую систему, при­менив к ней определенное преобразование, упрощают. Модель такой системы называется гомоморфной. Исследование систем управления всегда основывается на гомоморфных моделях. Рассмотрим основные виды гомоморфных моделей, используемых в исследовании проблем управления (рис. 3.1).

Гомоморфные модели могут быть материальными и абстрактными. Материальные модели — это воспроизведение основных геометричес­ких, физических, динамических и функциональных характеристик изу­чаемого объекта. Материальные модели включают физические и анало­говые модели. К абстрактным относят математические, имитационные и семиотические модели. На основе принципов построения абстракт­ных и аналоговых моделей создаются структурные модели. Важный класс представляют собой кибернетические модели, являющиеся синте­зом структурных и математических моделей.

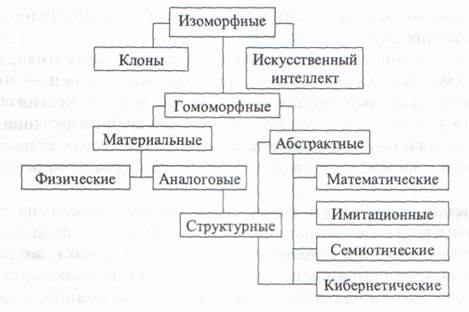
Рис. 3.1. Обобщенная классификация моделей

Дадим краткую характеристику общих классов моделей (рис. 3.1).

Физические модели представляют то, что исследуется с помощью уве­личенного или уменьшенного описания объекта или системы. Как ука­зывает К. Шеннон, «отличительная характеристика физической (пор­третной) модели состоит в том, что в некотором смысле она выглядит как моделируемая целостность (макет завода, здания, машины, систе­мы и т.д.)» [119]. К физическим относятся и модели биологических (жи­вых) систем. Физическая модель обладает следующими свойствами:

• содержит полный информационный базис — все факторы;

• отражает механизм действия объекта исследования;

• использует легко интерпретируемые функциональные зависимо­сти.

Аналоговая модель представляет исследуемый объект аналогом, ко­торый ведет себя как реальный объект, но не выглядит таковым. К ана­логовой модели любой системы можно отнести географическую карту, структурную и структурно-функциональную модели системы, законо­мерности и зависимости, построенные на основе принципа эквива­лентности и теории подобия. Особенности аналоговых моделей в со­поставлении с физическими моделями заключаются в следующем:

• необязательно содержится полный информационный базис, часть факторов может отсутствовать и часто заменяется други­ми, коррелированными с ними;

• опорная функция, выражающая точную физическую закономер­ность, как правило, описывается зависимостью, удобной для аппроксимации (замены математических объектов), и не подда­ется простой интерпретации.

Если при описании модели используется язык математики, то го­ворят о математических моделях. Математическая модель — это по­ставленный в соответствие реальному объекту математический объект (например, дифференциальная, линейная, нелинейная функции), ис­следование которого математическими методами позволяет получить полезные рекомендации относительно рассматриваемого реального объекта.

Математические модели отображают изучаемые объекты (процессы, системы) в виде явных функциональных соотношений: алгебраических равенств и неравенств (линейные модели), интегральных и дифферен­циальных, конечно-разностных и других математических выражений (закон распределения случайной величины, регрессионные модели и т.д.), а также отношений математической логики.

В зависимости от двух фундаментальных признаков построения математической модели — степени определенности исходной информации и изменений ее во вре­мени — различают детерминистические и стохастические, статические и динамические модели (рис. 3.2). Цель схемы, представленной на рис. 3.2, — отобразить следующие особенности:

• математические модели могут быть и детерминистическими, и стохастическими;

• детерминистические и стохастические модели могут быть и статическими, и динамическими.

Рис. 3.2. Классы математических моделей

Математическая модель называется детерминистической, если все ее параметры и переменные являются однозначно определяемыми ве­личинами, а также выполняется условие полной определенности информации. В противном случае, в условиях неопределенности инфор­мации, когда параметры и переменные модели — случайные величи­ны, модель называется стохастической. Модель называется динами­ческой, если как минимум одна переменная изменяется по периодам времени, и статической, если принимается гипотеза, что переменные не изменяются по периодам времени.

Имитационная модель — это алгоритмическое описание процесса функционирования системы на основе установленных статистических, аналитических и логических зависимостей, предназначенное для ис­следования реальных объектов путем численного эксперимента на ком­пьютере.

С развитием машинных, или вычислительных, экспериментов мо­дели, позволяющие воспроизвести функционирование системы на компьютере, например, динамические модели, стали называть имита­ционными, а имитацией — любой численный эксперимент на компью­тере с активным участием лица, принимающего решение [65].

Построение «чистой» имитационной модели представляется весьма сложным делом. Особенность его состоит в том, что процесс функци­онирования системы раскладывается на элементарные составляющие операции с сохранением логической структуры и последовательнос­ти их протекания во времени. Для каждой операции задается закон распределения изменения ее параметров, а для системы в целом — про­должительность периода проведения эксперимента. Разработать полез­ную имитационную модель непросто: от замысла до первых экспери­ментов лежит длинный путь проектирования и создания программного и информационного обеспечения и не меньший — от предваритель­ных экспериментов до содержательных научных результатов.

Под структурной моделью понимается формальный образ объекта (или системы), представленный в виде графической конструкции, состоящей из множества элементов и действующих между ними связей и построен­ной на основе определенных принципов, закономерностей и правил.

Семиотические модели — это модели теории информации, отобра­жающие свойства знаковой системы. Основные из них — инфологические (прагматические), семантические и синтаксические модели, создающие информационное и программное обеспечение для вычис­лительного процесса, и логико-лингвистические.

В особый класс выделяются кибернетические модели — агрегаты или агрегатные модели [8]. Они состоят из четырех основных элементов:

1) множества входных сигналов;

2) вектора состояния системы;

3) множества выходных сигналов;

4) множества управляющих сигналов — математических отноше­ний, связывающих все три элемента модели.

На их основе формируются модели систем как совокупность агре­гатных моделей, находящихся в некотором отношении друг с другом. Модель системы называют детерминистической, если каждой реали­зации ее входного сигнала соответствует одна реализация выходного сигнала, и стохастической — если каждой реализации ее входного сиг­нала соответствует вполне определенное распределение ее выходного сигнала.

На основе выделенных общих классов моделей строятся классы специальных моделей, ориентированных на управление организация­ми. Ниже изложим их особенности.

Date: 2015-10-19; view: 864; Нарушение авторских прав