Специальные классы математических и имитационных

Моделей

К настоящему времени накоплен достаточно большой арсенал ма­тематических и имитационных моделей специального приложения — это модели экономики, управления и прогноза (рис. 3.3). Следует от­метить, что рассматриваемое разделение моделей общепринято, хотя и существует некоторая условность, так как любое исследование с при­менением моделей в качестве результата выдает прогноз. Кроме того, решения в сфере экономической деятельности являются исходными для управления организациями, так же как решения в сфере управле­ния служат входной информацией для оценки экономической эффек­тивности работы организации. Выделенные классы моделей могут ис­пользоваться совместно, но на разных этапах решения управленческих задач и проблем.

Рис. 3.3. Классификация моделей

Модели экономики, или экономические модели, по определению, данному в работе [124], — это описание математическим языком свойств (содержания, функционирования) процессов для установле­ния количественных и логических зависимостей между различными элементами экономических систем. К моделям экономики причис­ляют (рис. 3.3): балансовые (модели линейной алгебры), эконометрические, экономико-математические, экономико-статистические (система регрессионных уравнений, сведенная к общей задаче линей­ного программирования). Каждый класс моделей использует соответ­ствующий математический аппарат и имеет определенную сферу приложения.

Экономические модели являются базовыми для народнохозяйствен­ного, территориального, отраслевого, стратегического и тактического планирования. В этой связи модели экономики рассматриваются в основном в контексте планирования. Модели планирования опираются на аппарат линейной алгебры, линейное и нелинейное программиро­вание, математическую статистику и направлены на оптимальную увяз­ку производства и потребления различного вида ограниченных ресур­сов. Наиболее распространенные классы моделей планирования — модели математического программирования, которые представляют­ся линейными и нелинейными системами равенств и неравенств.

Модели управления служат для определения оптимальной траекто­рии достижения системой поставленной цели при наложении некото­рых ограничений на управление ее поведением и движением. В этом случае модели управления описывают различного рода экстремальные задачи оптимального управления динамическими системами. В тео­рии управления организациями наблюдается развитие этого класса моделей в связи с исследованием таких свойств систем, как устойчи­вость, управляемость, а также с развитием исследования динамики си­стемы, представляемой движением материальных, финансовых и ин­формационных потоков.

Существует и другое, наиболее развитое направление в понимании моделей управления — это модели организационного управления, к которым относят широкий спектр моделей исследования операций. Эти модели следует первоначально разделить укрупненно по таким призна­кам, как

­ метод поиска решения,

­ вид функции,

­ полнота и характер исход­ных данных,

­ пояснением концепции их применения.

Основные классы моделей организационного управления следу­ющие:

1) оптимизационные — линейные (система линейных равенств и неравенств), нелинейные (система нелинейных и линейных равенств), сетевые, стохастические модели (система равенств и неравенств с ве­роятностными переменными и ограничениями).

Оптимизационные модели применяются для объемного и календар­ного планирования, управления запасами, распределения ресурсов и работ, замены, параметризации и стандартизации оборудования, рас­пределения потоков товарных поставок на транспортной сети и дру­гих задач управления;

2) ориентированные на оценку параметров процессов и системы в целом — модели теории массового обслуживания и марковских про­цессов, описывающие процессы массового спроса на обслуживание с учетом случайного характера поступления требований и продолжитель­ности обслуживания

Назначение моделей теории массового обслуживания состоит в том, чтобы на основе информации о входящем случайном потоке требова­ний предсказать возможности системы обслуживания, организовать наилучшее выполнение требований для конкретной ситуации и оце­нить, как это отразится на ее стоимости.

Модели марковских случайных процессов — система дифференци­альных уравнений, описывающих функционирование системы или ее процессов в виде множества упорядоченных состояний на некоторой траектории поведения системы. Этот класс моделей широко исполь­зуется при математическом моделировании функционирования слож­ных систем;

3) ориентированные на анализ реальной конфликтной ситуации и выбор наилучшей стратегии поведения субъекта — модели теории игр, конструкция которых зависит от назначения и условия проведения игр, например, игры подразделяются на бескоалиционные и коалицион­ные, статистические и рефлексивные, конечные и бесконечные

Модели теории игр служат для выбора оптимальной стратегии в ус­ловиях ограниченной случайной информации или полной неопреде­ленности. Игра — математическая модель реальной конфликтной си­туации, разрешение которой ведется по определенным правилам, алгоритмам, описывающим некоторую стратегию поведения лица, принимающего решение в условиях неопределенности. Различают «игры с природой» и «игры с противником». Исходя из ситуации опре­деляются методы и критерии оценки принятия решений. Так, при «играх с природой» применяют критерии: Лапласа, максиминный (кри­терий Вальда) и минимаксный, Гурвица и Сэвиджа и ряд других алго­ритмических правил. При «играх с противником» для принятия реше­ний используются платежные матрицы, максиминный и минимаксный критерии, а также специальные математические преобразования в свя­зи с тем, что лицу, принимающему решение, противостоит недобро­желательный противник;

4) оптимального управления — модели нахождения устойчивого функционирования динамических и квазидинамических систем, объектов

Модели оптимального управления ориентированы на выбор траек­тории и управляющего воздействия на объект, удовлетворяющих всем приведенным ограничениям при минимальных затратах на поведение и движение объекта, а в контексте управления — на его функциониро­вание. К основным элементам этого класса моделей относят:

­ вектор-функцию множества управляющих воздействий на объект в каждый момент времени или управления системой;

­ вектор-функцию некоторой траектории развития системы в те­чение заданного периода времени;

­ целевую функцию, представленную интегралом затрат на развитие системы при ее переходе из начального состояния в конечное.

Исходным условием построения модели служит предположение, что на заданном отрезке времени (t₀,T) имеются некоторые траектории развития экономической системы и допустимое множество управляю­щих воздействий в каждый момент времени t, t₀ 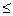t 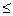T,a также задан­ные начальные и конечные условия развития системы. Математиче­ская теория оптимального управления сложными системами тесно связана с методами решения дифференциальных уравнений и опти­мизационными задачами в приложении к динамическим системам;

5) системной динамики — модели потоковых процессов, характеризующиеся переменными состояниями и скоростями потоков энергии, информации, промышленной продукции, денежных средств

В основе моделей системной динамики лежит представление о функционировании системы как совокупности потоков информации, энергии, материалов, продукции, денежных средств. Этот класс моде­лей предназначен для исследования как систем, функционирование которых по своей природе непрерывно, так и дискретных систем и процессов при высоком уровне агрегирования, где отображение их «природной» дискретности становится излишним. Переменные состо­яния и переменные скорости задаются системой разностных уравне­ний.

Модели прогноза — прогностические (статистические) функции раз­личного типа (рис. 3.3). К ним относят трендовые и регрессионные функции (монотонно возрастающие и монотонно убывающие функ­ции), функции роста и функции насыщения, функции одной перемен­ной и функции нескольких переменных и др. Выбор прогностической функции осуществляется с помощью методов математической статис­тики, теории вероятностей и теории прогнозирования.

Date: 2015-10-19; view: 507; Нарушение авторских прав