Основні теоретичні відомості

У процесі експлуатації параметри системи автоматичного регулювання можуть змінюватися в широких межах під дією зовнішніх умов і в результаті тривалої експлуатації. Діапазон припустимих змін цих параметрів, при яких не порушується стійка робота системи, можна визначити шляхом побудови областей стійкості в площині параметрів системи.

Якщо характеристичне рівняння системи описується поліномом третього порядку:

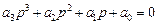, (9.1)

то найбільш зручним для аналізу таких систем є критерій стійкості І.А.Вишнеградського.

Пронормуємо рівняння (9.1):

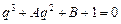, (9.2)

де ; .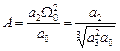

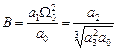На площині параметрів А і В (яка називається діаграмою Вишнеградського) нанесемо границі стійкості та границі переходу системи з одного стану в інший (рис. 9.1, а).

математичними виразами:

- криві СЕ і СF: ; (9.3)

- крива СD: 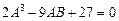, 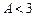; (9.4)

- границя стійкості: АВ = 1 при А>0 и В >0. (9.5)

В точці С, де А = 3 і В = 3, характеристичне рівняння (9.1) приймає вигляд 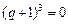, де ; .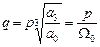

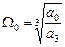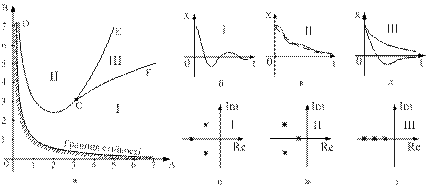
Рис. 9.1 Діаграма Вишнеградського (а), вигляд перехідних процесів (б, в, д) та розташування коренів (е, ж, з) характеристичного рівняння третього порядку.

Кожна крива на діаграмі Вишнеградського (рис. 9.1) описується

Запас стійкості - це кількісна характеристика, і його наявність гарантує стійкість автоматичної системи. Запас стійкості САК по амплітуді 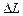і по фазі 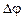можуть бути знайдені по ЛАЧХ і ФЧХ розімкненої системи (рис. 9.2).

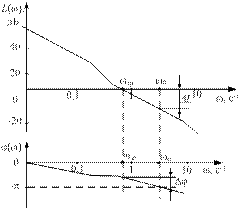
Рис. 9.2 Визначення запасу стійкості САК по ЛАЧХ і ФЧХ розімкненої системи

Date: 2015-10-19; view: 520; Нарушение авторских прав