Квантовые числа. Решение уравнения Шредингера позволяет найти волновые функции, при этом выяснено, что для полного определения каждого решения необходимы три целых числа –

Решение уравнения Шредингера позволяет найти волновые функции, при этом выяснено, что для полного определения каждого решения необходимы три целых числа – квантовые числа. Можно сказать, что квантовые числа описывают совокупность движений электронов в атоме.

ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n) определяет общую энергию электрона на данной орбитали и принимает значения n = 1, 2, 3, 4….

Чем больше n, тем больше объем внутреннего пространства атомной орбитали, т.е. растет удаленность электрона от ядра атома. Все электроны с одинаковым значением главного квантового числа образуют электронный слой. Приняты следующие обозначения электронных слоев:

Значение n ……………………………. 1 2 3 4 5 6 7

Обозначение слоя (уровня) ………….. K L M N O P Q.

Зная главное квантовое число можно определить максимальное число электронов, которое может находиться на этом уровне по формуле N_е = 2n².

Возможное число подуровней для каждого электронного уровня численно равно значению n– первый уровень (n = 1) состоит из одного подуровня, второй уровень (n = 2) – из двух и т.д. (табл.3).

ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (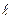), которое иногда называют побочным квантовым числом, определяет форму электронного облака и принимает значения от нуля до n-1. Область электронного уровня, в котором содержатся орбитали определенной формы называется энергетическим подуровнем. Подуровень, содержащий s-орбитали, называется s-подуровнем, р-орбитали - р-подуровнем и т.д. Например, при n = 1, 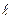= 0 (на первом уровне существуют только s-электроны). При n = 3, 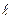= 0, 1, 2 (на третьем уровне содержит 3s-, 3р- и 3d-электроны).

Максимальное число подуровней и орбиталей на энергетических уровнях

Энергетический уровень	Число подуровней	Типы орбиталей	Орбитали,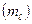
К (n = 1)		1s
L (n = 2)		2s 2p	-1, 0, +1
M (n = 3)		3s 3p 3d	-1, 0, +1 -2, -1, 0, +1, +2
N (n = 4)		4s 4p 4d 4f	-1, 0, +1 -2, -1, 0, +1, +2 -3, -2, -1, 0, +1, +2, +3

Если 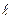= 0, электронное облако имеет сферическую форму (рис. 5);

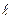= 1 - электронное облако имеет форму симметричной восьмерки (гантель, рис. 6). С ростом численного значения орбитального квантового числа форма электронного облака усложняется.

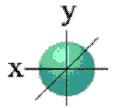
Рис. 6. S-облако. Рис. 7. Р-облака

МАГНИТНОЕ КВАНТОВОЕ ЧИСЛО 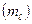характеризует ориентацию данной орбитали в пространстве. Магнитное квантовое число принимает целочисленные значения от - 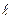до + 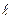, включая ноль. Например,для 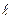= 2, магнитные квантовые числа имеют значения -2, -1, 0, +1, +2, т.е. в данной подоболочке (d-подуровень) существует пять орбиталей. Соответственно на s-подуровне ( 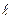= 0) имеется одна орбиталь; на р-подуровне ( 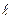= 1) – три орбитали; на f-подуровне – семь орбиталей. Атомную орбиталь обозначают в виде клеточки □. Тогда число орбиталей на соответствующих подуровнях будет равно: s-подуровень - □; р-подуровнь - □□□; d-подуровень - □□□□□; f-подуровнь - □□□□□□□.

Вышерассмотренные квантовые числа полностью характеризуют три определяющих свойства электрона-волны: длину, направление и амплитуду. Однако у электрона-частицы имеется особое свойство, называемое спином. Упрощенно спин можно рассматривать как вращение электрона вокруг собственной оси. Поэтому в теорию строения атома введено еще одно

СПИНОВОЕ КВАНТОВОЕ ЧИСЛО (m_s), которое может принимать два значения в соответствии с двумя возможными направлениями вращения:

m_s = + 1/2 (электрон вращается по часовой стрелке вокруг своей оси и имеет обозначение - ↑), m_s = - 1/2 (электрон вращается против часовой стрелки вокруг своей оси и имеет обозначение - ↓).

Date: 2015-10-19; view: 380; Нарушение авторских прав