Аркадий, Борис, Владимир и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу)

Сколько рукопожатий было сделано?

Решение:

Изобразим графически. В качестве вершин возьмем имена, а в качестве ребер – рукопожатия.

Б

G:

А В

Д

Ответом на вопрос задачи будет количество ребер в графе G.

Ответ: было сделано 6 рукопожатий.

Если вершина И является началом или концом ребра А, то говорят, что И и А инцидентны.

Пример.

2 4

И2 И5

И6

G: И1 3

И4 И3 5

1

Вершина 1 и ребро И4 инциденты.

Степенью (валентностью) вершины неориентированного графа называется число ребер , инцидентных данной вершине. Таблица степеней вершин данного графа имеет вид:

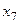
4.5.1 Способы задания графа.

Пусть граф G задан графически.

a5

a1 a2

2

G: 1 3

a3 4 a4

1) Матрицей смежности А_g=(Аij) графа G называется матрица размерности n (n-количество вершин в графе):

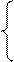Aij = 1, если (ai, aj)є R

С, если есть кратные ребра;

0, если (аi, aj)¢ R

где с - количество кратных ребер.

Для заданного графа G матрица смежности имеет вид:

2) Матрицей инцидентности BG = (Bij) графа G называется матрица размерности m n (где m количество строк, соответствующее количеству вершин в графе, n – количество столбцов, соответствующее количеству ребер в графе):

Bij=

Для заданного графа G матрица инцидентности имеет вид:

Расстоянием между вершинами и в неориентированном графе называется наименьшее число ребер, соединяющих эти вершины. Условный радиус графа относительно вершины определяется формулой:

.

Здесь – это множество вершин графа .

Радиус графа определяется как наименьший из условных радиусов графа, а центр графа составляют вершины, условные радиусы графа относительно которых совпадают с радиусом графа.

Для данного графа таблица расстояний и условных радиусов вершин имеет вид:

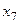
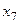
Радиус графа , следовательно, центр графа – это множество вершин .

Рассмотрим графы G₁ = (M₂, R₁) и G₂ = (M₂, R₂).

1 2 1 2

G1: G2: 3 4

3 4

5 6

5 6

1) Объединение графов G₁ и G₂, обозначаемое G₁ƯG₂, представляет собой такой граф (M₁ƯM₂, R₁ƯR₂), что множество его вершин является объединением М₁ и М₂, а множество ребер – объединением R₁ и R₂.

1 2

3 4

5 6

2) Пересечение графов G₁ и G₂, обозначаемое G₁∩G₂, представляет собой граф (M₁∩M₂, R₁∩R₂). Таким образом, множество вершин G₃ состоит только из вершин, присутствующих одновременно в графах G₁ и G₂, а множество ребер G₃ состоит только из ребер, присутствующих одновременно в G₁ и G₂.

1 2

G1∩G2: 3 4

5 ∙ 6

3) Кольцевая сумма графов G₁ и G₂, обозначаемая G₁+G₂, представляет собой граф G₃, порожденный на множество ребер R₁ +R₂. Другими словами граф G₃ не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G₁, либо в G₂, но не в обоих графах одновременно.

1 2

Литература:

[6] стр. 69-80

Date: 2015-10-19; view: 1158; Нарушение авторских прав