Дублетный характер спектров щелочных металлов

Гипотеза об электронном спине позволяет объяснить дублетный характер спектров щелочных ме­таллов. Формально дублетный характер линий щелочных металлов может быть объяснён, если предположить, что все термы этих элементов двойные за исключением. S-термов. Такое расщепле­ние термов вытекает из гипотезы о наличии у электрона спинового момента. В атомах щелочных металлов, благодаря возмущению орбиты валентного электрона в поле атомного остатка, каждой паре квантовых чисел п, l (п - главное квантовое число, l - орбитальное квантовое число) соот­ветствует определённый энергетический уровень. По теории Бора этой паре квантовых чисел п, l соответствует орбита валентного электрона определённых размеров и формы. Двигаясь по этой орбите, электрон обладает орбитальным механическим и магнитным моментами, т.е. возбуждает магнитное поле (магнитный момент атомного остатка в силу его высокой симметрии равен нулю). Принимая гипотезу о собственном моменте электрона, необходимо учесть возможные ориентации спинового момента относительно орбитального момента . Так как электрон, наряду с механи­ческим моментом , обладает связанным с ним собственным магнитным моментом μ₀, то придвижении возникает добавочная энергия ΔW', зависящая от относительной ориентации моментов и . Собственный момент электрона может ориентироваться относительно орбитального момента только двумя способами. Этим двум возможным ориентациям соответствуют два значения добавочной энергии ΔW', и, следовательно, расщепление каждого терма на два.

Гипотеза о наличии собственного магнитного момента у электрона объясняет и так называемую тонкую структуру линий водорода и сходных с ним ионов. Эта структура аналогична дублетной структуре линий щелочных металлов, но только значительно уже. Гипотеза о собственном магнитном моменте электрона объясняет аномалии в значениях маг­нитных моментов атомов и расщепление спектральных линий в магнитном поле более чем на три компонента.

3. Расчёт длин волн линий резонансного дублета натрия.

Теперь нам известно, что является причиной дублетного расщепления спектральных линий ще­лочных металлов. Попробуем описать это математически.

Энергия связи электрона с ядром описывается уравнением, напоминающее уравнение для стан­дартного терма щелочного металла:

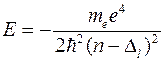. (1)

Запишем её в системе СИ (отличия лишь в коэффициенте) и учтём ещё добавочное вза­имодействие - взаимодействие спинового магнитного момента электрона с его орбитальным маг­нитным моментом (далее будем записывать все формулы используя систему СИ):

, (2)

где ε ₀ = 1 / 16 π².

Первый член этого соотношения - это энергия с учётом поляризации квазиядра и учётом того, что есть вероятность обнаружить электрон вблизи ядра. ΔW’ это поправка, учитывающая взаи­модействие спинового магнитного момента электрона с его орбитальным магнитным моментом. Задача сводится к расчёту расщепления энергии ΔW для этого типа взаимодействия. Энергия взаимодействия спинового магнитного момента с полем, в нашем случае это поле создаваемое орбитальным механическим моментом, как известно, описывается следующим выражением:

, (3)

где - спиновый магнитный момент электрона, - магнитная индукция поля созданного орби­тальным механическим моментом электрона, μ_Б – магнетон Бора.

Спиновый механический момент электрона квантуется по закону:

(4)

С учётом этого:

(5)

Из векторной диаграммы на рис. 1. по теореме косинусов следует:

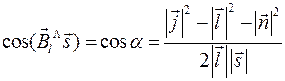(6)

,

- 78 -

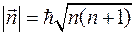. (7)

Для вычисления B_l определим магнитную индукцию поля, создаваемого круговым током I, радиуса r:

(8)

Магнитный момент витка тока площади S и силы тока I равен

(9)

отсюда 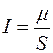. Выразив площадь , и подставив в (8), получим:

(10)

Магнитная индукция поля, создаваемого орбитальным магнитным моментом электрона:

, (11)

где орбитальный магнитный момент электрона:

(12)

Подставив (6), (7), (11), (12) в (5), получим:

(13)

Для электрона величина 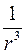не имеет физического смысла, необходимо брать среднее значение , которое в квантовой механике описывается выражением:

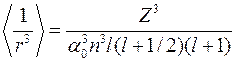, (14)

где:

(15)

Заменив в (13) на (14), получим:

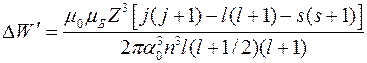(16)

Подставив известные значения, можно по (16) теоретически рассчитать ΔW’.

Таким образом, полная энергия электрона согласно (2) и (16) будет иметь вид:

(17)

Длина волны фотона, который излучается при переходе будет:

(18)

Для окончательного решения данной задачи необходимо учесть тот факт, что существует вероятность обнаружить электрон как снаружи квазиядра, так и внутри него. Таким образом, заряд ядра Z на самом деле нельзя считать равным количеству протонов в ядре. Он будет несколько меньше в связи с тем, что квазиядро экранирует ядро, и "эффективно" на электрон действуют не все протоны ядра. Для того чтоб учесть этот факт, вводят поправку, называемую коэффициентом экранирования α. Для атомов с порядковым номером больше 10 этот коэффициент приблизительно равен α ≈ 7.45. Тогда в конечную формулу для энергии нужно подставлять Z* вместо Z, где Z* = Z – α.

Так как определить длины волн дублета довольно легко, то задачу используют в обратном направлении. По измеренным значениям длин волн определяют коэффициент экранирования.

Для резонансного перехода атома натрия (α = 7.45) теоретически можно получить дублет с такими длинами волн:

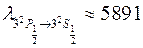Å Å

Энергетический зазор между этими двумя линиями составляет 1.2∙10^-3 эВ.

В данной работе необходимо экспериментально определить длины волн дублета натрия и найти значение коэффициента экранирования по формуле:

, (19)

где определяется по длинам волн дублета.

Date: 2015-10-19; view: 857; Нарушение авторских прав