Дифракция электронов

Физический смысл дифракции электронов заключается в том, что при прохождении пучка электронов через кристалл, они взаимодействуют с его кристаллической решёткой, в результате чего они рассеиваются по разным направлениям, которые зависят от строения решётки.

Узкий пучок электронов с одинаковой скоростью, а также, с одинаковой длиной волны проходит через тонкую плёнку исследуемого кристаллического объекта (рис.6). На экране, расположенном на некотором расстоянии от объекта, образуется дифракционная картина. Ширина пучка регулируется магнитной линзой и системой диафрагм. Монохроматизация пучка достигается качественной стабилизацией ускоряющего поля.

Известно, что в кристаллической решётке можно выбрать большое количество параллельных плоскостей, которые проходят через узлы ячеек. Для каждой выбранной системы плоскостей, расстояние между плоскостями есть величина постоянная.

Дифракцию электронов можно представить себе как результат отражения электронного пучка от атомных плоскостей кристаллической решётки. Направление отражённых, а точнее – дифрагированных электронов, зависит от ориентации отражающих кристаллографических плоскостей в пространстве и условий отражения, которые подчиняются закону Вульфа-Брега.

При пересечении дифрагированного пучка электронов с поверхностью экрана или фотопластинкою, получаются следы, которые в совокупности дают дифракционную картину. В зависимости от характера объекта и способа, которым получают дифракционную картину, она может складываться из отдельных отражений или линий.

Если электронный пучок падает на монокристалл, то дифракционная картина будет представлять собой систему отдельных отражений, где каждое отражение соответствует электронам, отражённым от плоскостей, которые имеют соответствующие значения индексов h k l (рис.7).

Рис.5. Кристаллографические плоскости отражения для кубического кристалла. Эти плоскости заштрихованы, а атомы, которые входят в них зачернены. На рис. а) отрезки по осям x и z равны ∞, а по оси y отрезку a. Поэтому указанная плоскость характеризуется тройкою цифр (010). На рис. з) плоскость с отрезками а/3, a/1, a/2 соответственно имеет индексы (312).

Рис. 6. Принцип работы электронографа.

Положение рефлексов в каждом отдельном случае будет зависеть от свойств атомной решётки исследуемого вещества. Дифракция на монокристаллах называется точечной (поскольку она складывается из отдельных рефлексов).

Рис.7. Схема дифракции электронов на монокристалле.

5. Расчёт межплоскостных расстояний по дифракционной картине.

Рассмотрим процесс формирования дифракционной картины более детально. Если пучок электронов падает на решётку кристалла, то благодаря волновым свойствам электрона на атомах решётки возникает дифракция. Представим сначала упрощённую модель явления. Пусть мы имеем ряд атомных плоскостей, которые находятся на расстоянии d одна от одной (рис.8). Как было показано Вульфом и Брегом, явление дифракции в кристалле можно свести к отражению волн от таких плоскостей. Два луча, падающих под углом скольжения q и отражённых от двух плоскостей, будут однофазны если разница хода между ними будет λ, 2λ, 3λ,... nλ. Условия однофазности для отражённых лучей записываются в виде известного соотношения Вульфа-Брега:

2d_hkl × sinq = nλ , (4)

где d_hkl - расстояние между кристаллографическими плоскостями с соответствующими индексами hkl (индексы Миллера).

Направление отражённого луча составляет с начальным угол 2q.

Если исследуемый объект представляет собой не монокристалл, а поликристаллическое вещество, то есть совокупность большого числа микроскопичных кристалликов, которые хаотично ориентированы в пространстве, то первичный луч, падая на объект, встречает на своём пути очень большое количество кристаллических плоскостей, для которых будет выполняться соотношение Вульфа-Брега. В этом случае, дифрагированные лучи, отражённые этими плоскостями, образуют серию конусов, ось которых будет совпадать с направлением падающего (первичного) луча. При пересечении этих конусов с экраном или с фотопластинкою, расположенных перпендикулярно

падающему лучу, получим концентричные кольца (рис.9).

Диаметры D этих колец, образованных отражёнными от хаотично расположенных плоскостей с разными значениями индексов hkl, связаны с углом дифракции следующим соотношением:

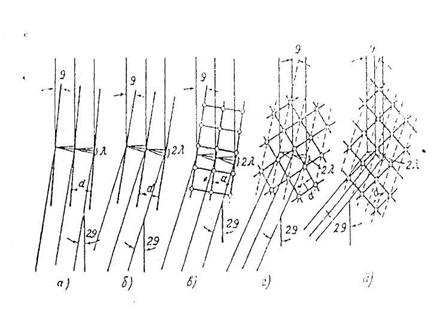
Рис.8. Отражения от параллельных плоскостей кристаллической решётки: а) разность хода λ (n = 1); б) разность хода 2λ (n = 2); в) отражения от граней элементарного куба; г) отражения от диагональных плоскостей элементарного куба. Отражающие плоскости на рисунках а), б) и в) показаны сплошными линиями, а на рисунках г) и д) – пунктирными.

tg2q = 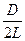, (5)

где L – расстояние от объекта до экрана или до фотопластинки.

Так как углы дифракции обычно не превышают 4^°, то замена sinq или tgq на угол q даёт лишь небольшую ошибку, поэтому можно записать, что q = D/L и тогда соотношение Вульфа-Брега можно записать:

d_hkl × D = 2nλL (6)

Если записать (6) через радиусы колец, то получим:

d_hkl × R = nλL (7)

Date: 2015-10-19; view: 1360; Нарушение авторских прав