
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема: Побудова лінійної багатофакторної моделі з урахуванням мультиколінеарності
|
|
Мета заняття: Задана вибірка, отримана для факторів X1, Х2, Х3 і показника Y. Необхідно:
ü знайти кореляційну матрицю;
ü використовуючи  –критерій з надійністю Р=0,95 перевірити систему факторів на існування загальної мультиколінеарності;
–критерій з надійністю Р=0,95 перевірити систему факторів на існування загальної мультиколінеарності;
ü у випадку існування загальної мультиколінеарності, використовуючи t-статистику виявити пари мультиколінеарних факторів; якщо такі пари існують, виключити один із цих факторів;
ü знайти оцінки параметрів лінійної регресії, результат отриманих оцінок перевірити, використовуючи сервіс: статистика/линейн;
ü використовуючи F-критерій з надійністю Р=0,95, перевiрити статистичну значущість коефіцієнта детермінації (оцінити адекватність прийнятої моделі статистичним даним).
Якщо математична модель із заданою надійністю адекватна експериментальним даним, то:
ü використовуючи t-критерій, з надійністю Р=0,95 оцінити значущість параметрів регресії;
ü знайти значення прогнозу показника для заданих значень факторів;
ü його довірчий інтервал з надійністю Р=0,95;
ü частинні коефіцієнти еластичності для точки прогнозу.
Хід роботи
- Завантажити програму EXCEL.
- Вихідні даних факторів розміщуємо у блоці В3:В17, а показника в стовпці Е3:Е17 (рис.1).
Перевіримо систему факторів на мультиколінеарність, зробивши розрахунки згідно алгоритму Фаррара-Глобера:
- Знайдемо кореляційну матрицю та розмістимо її у блоці А23:С25.
Її можна знайти нормалізуючи статистичні дані за формулою:  , де n - число розглянутих періодів, m -число факторів,
, де n - число розглянутих періодів, m -число факторів, 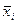 - середнє значення фактора Хi,
- середнє значення фактора Хi,  - середньоквадратичне відхилення фактора Хi.
- середньоквадратичне відхилення фактора Хi.
При нормалізації статистичних даних використаємо вбудовану функцію СРЗНАЧ (блок В21:Е21); СТАНДОТКЛОНП (блок I27:I29) і вбудовану функцію КОРЕНЬ для розрахунку у комірці А21  .
.
Нормалізовані статистичні дані формуємо у блоці F3:Н17 (рис.1).
(Слід зазначити, що нормалізовані статистичні дані можна знайти за формулою:  ).
).
Для розрахунків елементів кореляційної матриці використовуємо вбудовану функцію СУММПРОИЗВ. Елемент кореляційної матриці, який знаходиться у i-му рядку та j-му стовпці, знайти таким чином: СУММПРОИЗВ стовпцянормалізованих статистичних даних i-го фактора й стовпцянормалізованих статистичних даних j-го фактора.
(Кореляційну матрицю можна знайти, використовуючи послідовно вбудовані функції: ТРАНС (блок матриці) та МУМНОЖ (блок даних першої матриці; блок даних другої матриці) за формулою 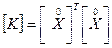 , де
, де 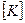 - кореляційна матриця,
- кореляційна матриця, 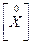 - матриця нормалізованих статистичних даних блоку F3:Н17,
- матриця нормалізованих статистичних даних блоку F3:Н17, 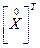 - транспонована матриця стосовно матриці
- транспонована матриця стосовно матриці 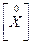 .
.
 |
Або не нормалізуючи статистичні дані, а використовуючи вбудовану функцію КОРРЕЛ (коефіцієнт кореляції між двома однорідними множинами даних.)
- Знайдемо визначник матриці |К| і запишемо результат у комірці Е24, використовуючи вбудовану функцію МОПРЕД.
- Обчислимо розрахункове значення критерію
 за формулою:
за формулою: 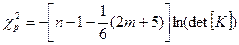 , де n – об’єм вибірки (n=15), m - число факторів моделі (m=3) та розмістимо результат у комірці Е25:=-(14-11/6) *LN(E24).
, де n – об’єм вибірки (n=15), m - число факторів моделі (m=3) та розмістимо результат у комірці Е25:=-(14-11/6) *LN(E24). - Знайдемо табличне (критичне) значення критерію
 і запишемо результат у комірці E26, використовуючи вбудовану функцію ХИ2ОБР (імовірність a=0,05, число ступенів вільності k=m(m-1)/2=3(3-1)/2=3).
і запишемо результат у комірці E26, використовуючи вбудовану функцію ХИ2ОБР (імовірність a=0,05, число ступенів вільності k=m(m-1)/2=3(3-1)/2=3). - Зробимо висновки про наявність загальної мультиколінеарності (рис.2).
Визначимо мультиколінеарні пари факторів за допомогою t-статистики (критерію Стьюдента):
- Знайдемо матрицю С, обернену до кореляційної, розмістивши результат у блоці А27:С29.
-
 Розрахуємо частинні коефіцієнти кореляції між парами факторів за формулою:
Розрахуємо частинні коефіцієнти кореляції між парами факторів за формулою:  , де сkj - елемент матриці С, що лежить у к-му рядку й j-ому стовпці, cкк й cjj - діагональні елементи матриці С, записавши отримані результати у комірки Е27:Е29 відповідно.
, де сkj - елемент матриці С, що лежить у к-му рядку й j-ому стовпці, cкк й cjj - діагональні елементи матриці С, записавши отримані результати у комірки Е27:Е29 відповідно. - Обчислимо розрахункові значення t-статистик за формулою:
 , де rkj - частинні коефіцієнти кореляції між парами факторів та запишемо отримані результати у комірки G27:G29 відповідно.
, де rkj - частинні коефіцієнти кореляції між парами факторів та запишемо отримані результати у комірки G27:G29 відповідно. - У комірці G26 обчислимо табличне (критичне) значення t-статистики, з використанням вбудованої функції СТЬЮДРАСПОБР (імовірність a=0,05, число ступенів вільності k=n-m-1=15-4=11).
- Зробимо висновок про наявність мультиколінеарності між парами факторів (рис.2).
- Виключимо один з факторів, між якими існує мультиколінеарність (у нашому випадку Х3). Для цього у блоці F23:G24 знайдемо кореляційну матрицю факторів, що залишилися. Обернену матрицю знайдемо у блоці H23:I24 (рис.2), а визначник цієї матриці обчислимо у комірці В38, розрахункове значення Xi2- у комірці В39, а табличне (критичне) значення
 – у комірці В40 (рис.3).
– у комірці В40 (рис.3). -

Порівняємо отримані результати та зробимо висновок про наявність мультиколінеарності між факторами.
Припустимо, що між показником Y і факторами X1 й X2 існує лінійна залежність Y=a0+ a1 X1+ a2 X2 . Знайдемо оцінки параметрів, використовуючи матричні операції. Для оцінки параметрів вектора  використаємо формулу
використаємо формулу  .
.
Date: 2015-10-19; view: 590; Нарушение авторских прав