Хід роботи. - експоненціальної (рис

1. Завантажити програму EXCEL.
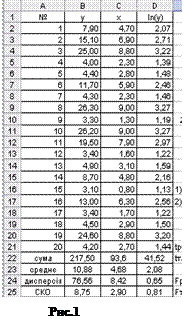
2. Сформувати таблицю вихідних даних, заповнивши діапазон комірок А2:C21 (рис.1).
3. За допомогою майстра побудови діаграм побудувати кореляційне поле даної статистичної вибірки (див. рис.2)
4. По виду кореляційного поля (так як з ростом х - у в основному збільшується) припускається наявність залежності двох типів:

- лінійної ;

- експоненціальної 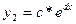(рис. 2).

1. Для побудови гіпотези про вид залежності необхідно виконати розрахунки:

5.1. У комірці В27 за допомогою вбудованої функції СЧЕТЗ знайдемо об’єм вибірки n;

5.2. Розрахуємо значення натурального логарифма величини y, використовуючи вбудовану функцію LN і результати обчислення розмістимо у діапазоні D2:D21;

5.3. Розрахуємо суму величин , 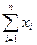та 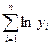, використовуючи вбудовану функцію СУММ або Автосумму;

5.4. Розрахємо середнє значення величин y, x, ln(y ), використовуючи вбудовану функцію СРЗНАЧ;

5.5. Розрахуємо дисперсію величин y, x, ln(y ), використавши при цьому вбудовану функцію ДИСП;

5.6. Розрахуємо середнє квадратичнє відхилення (СКВ) величин y, x, ln(y), як корінь квадратний з дисперсій відповідних величин, використавши при цьому вбудовану функцію КОРЕНЬ (рис. 1).

1. Обчислимо вибіркові парні коефіцієнти кореляції між x й y та x й Ln(y) за формулою , або використовуючи вбудовану функцію КОРРЕЛ, розмістивши результати обчислень у комірках F3, G3 відповідно (мал. 4).

За знайденими значеннями коефіцієнтів зробити висновки.

1. Обчислимо для одержання лінійної залежності величин x й y: Y=ax+b, коефіцієнти а й b за формулами: і , зробивши наступне:

- розрахуємо коефіцієнт a, ввівши у комірку G6 формулу G6:=F3*(B25/C25);

- розрахуємо коефіцієнт b, ввівши у комірку G7 формулу G7:=B23-(G6*C23).

1. Записати отриману лінійну залежність у діапазоні Е8:I8 (рис.3).
2. Для одержання експоненціальної залежності величин x та y: Y=c*e^d*X необхідно розрахувати коефіцієнти c й d. Перед цим прологарифмуємо рівняння: ln(Y)=ln(c)+d*X і здійснивши відповідні заміни z=ln(Y) і f=ln(c), одержимо лінійну залежність виду z=f+dх. Розрахуємо коефіцієнти f й d (використаємо аналогічні формули для лінійної залежності):

- розрахуємо коефіцієнт d, ввівши у комірку G11 формулу G11:=G3*(D25/C25);

- розрахуємо коефіцієнт f, ввівши у комірку G12 формулу G12:=D23-(G11*C23).

1. Так як f=ln(c), то 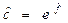, то розрахуємо оцінку параметра с, ввівши у комірку G13 формулу G13:=EXP(G12), використовуючи вбудовану функцію EXP.
2. Записати отриману експоненціальну модель у діапазоні Е14:I14 (рис.3).
3. Обчислимо розрахункове значення y_i1розр для лінійної залежності Y=aх+b. Для цього у комірку J2 ввести формулу J2: =$G$6*C2+$G$7, використовуючи абсолютне посилання для комірок G7 и G6.
4. Використовуючи операцію автозаполнення, скопіювати формулу у діапазон J3:J21.
5. Стовпець К розрахуємо як квадрат різниці (y_i - y_i1розр)² , ввівши у комірку К2 формулу К2:=(В2-J2)^2. Використовуючи операцію автозаполнения, скопіювати формулу у діапазон К3:К21.
6. Обчислимо розрахункове значення y_i2розр для експоненціальної залежності Y=c*e^d*X. Для цього у комірку L2 введемо формулу L2:=$G$13*(EXP($G$11*C2)), використовуючи вбудовану функцію EXP й абсолютне посилання для комірок G13 и G 11.
7. Стовпець M розрахуємо як квадрат різниці (y_i - y_i2розр)² , ввівши у комірку M2 формулу M2:=(В2-L2)^2. Використовуючи операцію автозаполнення, скопіювати формулу у діапазон M3:M21.
8. У комірках K22 й M22 розрахуємо суму всіх значень y_i1розр й y_i2розр, використовуючи вбудовану функцію СУММ або Автосумму (рис. 4).
9. Розрахуємо дисперсії залишків для лінійної й експоненціальної залежностей, використовуючи формулу: 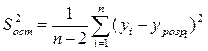. Для цього у комірку G16 введемо формулу G16:=К22/(В27-2), а у комірку G17:=М22/(В27-2) (рис.3).
10. Порівняємо дисперсії залишків даних залежностей. Тепер можна зробити висновок про те, яка модель краще відображає задану залежність.

Date: 2015-10-19; view: 348; Нарушение авторских прав