
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Конструирование шкалы как эталона измерения
|
|
Нахождение эталона измерения осуществляется в четыре стадии, каждая из которых – необходимая предпосылка надежности будущей шкалы.
1. Качественная классификация объектов (измеряемых свойств). Собираясь, например, измерять структуру ценностных ориентаций личности, мы прежде всего должны четко классифицировать типы ориентаций, исходя из теоретической концепции и задач исследования. Можно положить в основу классификации иерархию потребностей или интересов, сфер деятельности, социальные функции ориентаций, социальные ситуации, которые бы различались по степени свободы выбора целей и средств деятельности и т.д.
2. Поиск протяженности выделенных в качественном анализе свойств. Следует установить, обладают ли эти свойства прерывной или непрерывной протяженностью? Можно ли их представить в виде различных последовательных состояний измеряемого качества? Например, определенная ценностная ориентация (материальный достаток, творчество и т.п.) могут быть представлены как градации, отражающие ее “протяженность”: “сильная/средняя/слабая ориентация”, “устойчивая/малоустойчивая/неустойчивая”, “центральная/периферийная”.
3. Установление эмпирических индикаторов или внешних признаков тех свойств объекта, которые поддаются расположению в континуум. Индикатор – это внешне хорошо различимый показатель измеряемого признака. С его помощью устанавливается наличие или отсутствие признака, его состояние. Например, высота ртутного столбика термометра – индикатор температуры.
Простейший индикатор расположения какого-то объекта среди других объектов – порядковое место, отмечаемое опрашиваемым в заданном списке. Например, из 18 объектов он помечает объект М порядковым номером “1”. Этот номер – индикатор доминирования объекта М. Объект N, помеченный порядковым номером “18”, будет располагаться в конце протяженности (“подавленная ориентация на N”).
Сложнее найти индикатор для протяженности по критерию “сильные”, “средние”, “слабые” ориентации. Один из возможных вариантов таков.
Испытуемым предлагают три ситуации, в которых они принимают решение о выборе “ценностного ориентира”. Ситуации различаются по степени свободы выбора “ценностного ориентира”. Допустим, измерению подлежат интересы к различным видам занятий в сфере досуга. Предлагаются три одинаковых списка возможных занятий, число которых в каждом списке 18.
В первой ситуации (широкий выбор диапазона) испытуемый имеет право без ограничения указать любые занятия, которые ему нравятся. Во второй ситуации (средний диапазон выбора) он оставляет в списке лишь шесть наиболее важных для него занятий, в третьем случае (узкий диапазон) – не более трех, для него особенно значимых.
Индикатор “сильной” ориентации – выбор данного занятия – имел место во всех трех ситуациях; “средний” – выбор в первой и второй ситуациях, “слабый” – выбор имел место только при широком диапазоне принятия решения.
4. Уяснение того, все ли единицы, составляющие измеряемый объект, укладываются в ранжируемый ряд, все ли они обладают свойством занимать определенное место в континууме отношений по принятым индикаторам.
В итоге описанных операций устанавливается эталон или шкала измерения. Отношения между пунктами шкалы должны отображать отношение свойств объекта в понятиях “равно”, “больше”, “меньше”.
Способы проверки процедуры первичного измерения на надежность.
Понятие надежности измерения правомерно относить именно к инструменту, с помощью которого производится измерение, но не к самим данным, подлежащим измерению. В отношении данных, как и заключительных выводов из обследования (исследования), правильнее говорить, что они достоверны (или относительно достоверны) и потому, что фиксированы надежным инструментом.
Надежность шкалы, как обобщающей характеристики инструмента измерения, может быть рассмотрена в трех аспектах: обоснованность, устойчивость, правильность.
Обоснованность (синоним валидности) шкалы заключается в том, что с ее помощью целенаправленно измеряют вполне определенное свойство или признак, не смешивая его с другими. Вполне справедливо выделяют два существенно разных аспекта обоснованности: теоретический и практический. Первый (теоретический) непосредственно связан с содержательными предпосылками исследования и предполагает установление значимых связей с широким классом ситуаций, предсказываемых теорией, второй требует доказательства надежной регистрации данных в сравнительно узком секторе, в частном проявлении изучаемых объектов. Если валидность эмпирическую через измерение обеспечивают, то валидность теоретическую только проверяют, т.е. уточняют область валидности методики, границы интерпретации получаемых материалов.
Чтобы повысить обоснованность измерения, используют ряд технических приемов:
а) Логические рассуждения на основе опыта и здравого смысла. Логические рассуждения хотя и являются достаточно хорошим средством повышения обоснованности, но не являются прямым доказательством того, что мы измеряем искомое свойство.
б) Тест по “эталонной группе”. Смысл проверки – в сопоставлении данных, полученных путем измерения по шкале, с достоверными сведениями об объекте измерения. Так, шкала на отношение к соблюдению норм права обосновывается опросом осужденных правонарушителей в сравнении с “эталонной” группой законопослушных граждан. Дихотомизация полярных групп по шкале должна совпадать с фактической поляризацией эталонных групп в пределах допустимой ошибки, величина которой зависит от задач исследования.
в) Поиск независимого критерия как разновидность внешнего контроля надежности для измерения того же самого объекта или свойства. Если бы был возможен такой прибор, который объективно фиксировал интенсивность мнений человека относительно опрашиваемых событий, фактов, других людей и т.п., то данный прибор бы выступал в роли независимого критерия, позволяющего сопоставлять с ним субъективные мнения, ощущения, настроения человека.
В качестве независимого критерия зачастую выступают объективные показатели эффективности деятельности и учебы: количество продукции, наличие ошибок, средний балл по учебным предметам и т.п. (подробнее смотри в параграфе 4.2.).
г) Использование метода судей для отбора пунктов шкалы. Сомнения в обоснованности возникают уже на стадии первоначального отбора пунктов шкалы. Численность судей (участвующих в отборе пунктов: например, определении единиц измерения) зависит от меры однородности или разнородности выборочной совокупности основного обследования. Рекомендуется отбирать для судейства половину мужчин и половину женщин.
д) Совмещение нескольких показателей для регистрации определенного одного свойства или построение индекса. Типы индексов крайне разнообразны. Суть индексной обоснованности в том, что согласно гипотезе, данному свойству находится множество его проявлений, для каждого из которых формируют отдельную шкалу.
Затем измерения по частным шкалам либо суммируются, либо из них образуют логические конструкции (например, логический квадрат).
Устойчивость измерения выражается в однозначности информации, которую мы извлекаем с помощью данной процедуры. Нередко устойчивость ошибочно отождествляют с надежностью процедуры в целом. И хотя последняя зависит не только от устойчивости, но также от обоснованности и правильности операций, подобное смешение не случайно: проверка инструмента на устойчивость – важнейшее условие повышения его надежности.
Приемы контроля на устойчивость:
а) Повторное измерение. Один и тот же объект, свойство измеряется дважды с двух-трехнедельным временным интервалом и с помощью одинаковой процедуры. Шкала считается устойчивой, если совпадения между первой и второй сериями измерений будут достаточно высокими. Так, вычисляется общий процент совпадений ответов в первой и второй сериях. Те пункты шкалы, в которых обнаружено несовпадение даже у весьма “устойчивых” субъектов, должны быть переформулированы.
Другим показателем полной устойчивости является мера сдвига, оцененная как среднеарифметическая ошибка различения градаций шкалы. Этот показатель означает, какую долю градации данной шкалы (в среднем) все испытуемые как бы не улавливают, т.е. каковы истинные границы различения градаций.
Например, уточним среднеарифметическую ошибку в различении трехчленной шкалы согласия-несогласия с каким-то суждением (пусть это будет суждение о привлекательности некоторого занятия на досуге). Из 28 человек, участвующих в испытании 17 полностью повторяют свои оценки данного занятия в обеих пробах, (сумма по диагонали схемы: 7 + 6 + 4 = 17), а остальные 11 испытуемых дают разные ответы в двух пробах.
| Ответы в первой пробе о занятиях на досуге | Ответы во второй пробе | |||
| Привлекает | Не очень | Не привлекает | Всего | |
| Данное занятие привлекательно (1) | - | |||
| Не очень привлекательно | ||||
| Не привлекательно | - | |||
| Всего |
Для оценки искомой ошибки вычисляем отличия ответов респондентов как сдвиги между II и I пробами, например, во II пробе из тех, кто в I пробе ответил “занятие привлекательно”, 3 человека сообщили, что оно “не очень привлекательно”, т.е. это разность (2 – 1). Теперь суммируем все разности в ответах испытуемых и получим меру среднеарифметической ошибки различения пунктов градации данной шкалы:
Ср.арифм.ошибка = 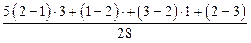 = 0,39 градации
= 0,39 градации
Значит, среднеарифметический “сдвиг” в оценке по трехчленной шкале составляет около 40% одного ее деления, т.е. менее половины деления, что в общем можно признать удовлетворительным, хотя и не идеальным.
Рассматривая устойчивость как воспроизводимость результатов измерений, можно использовать и иные показатели ее меры наряду с обычными расчетами корреляции итогов двух последовательных измерений.
Какая же мера устойчивости удовлетворительна? Это зависит от существа измеряемого свойства, его значимости для целей и задач исследования. В принципе для немногочленной шкалы среднеарифметическая ошибка различения градаций в 40% ее деления невысока, а соответствующая мера устойчивости (100% – 40% = 60%) вполне достаточна, ибо не перекрывает границы между двумя соседними интервалами шкалы, то ошибка была бы явно недопустима, ибо не перекрываются границы между двумя соседними интервалами шкалы. Если бы неустойчивость составила не 40%, а 60%, т.е. более половины деления шкалы, то ошибка была бы явно недопустима, ибо в среднем испытуемые не различают соседние градации из трех.
Для многочленных шкал, например из 10 градаций, ошибка в 60% одного деления не слишком велика, так как перекрываются два деления из 10, т.е. не 2/3, а 0,2 общей “длины” шкалы. Если при обработке данных градации укрупнить, объединяя две соседние, то ошибка минимизируется до вполне уверенного уровня устойчивости.
Помимо показателей полной устойчивости шкалы возможны также показатели ее относительной устойчивости. Они полезны при сравнении разных шкал, например для выбора из нескольких вариантов наиболее правильной и точной шкалы или для того, чтобы сопоставить уровни устойчивости измерения разных свойств, каждое из которых фиксируется шкалами разного типа и разной степени дробности.
б) Использование нескольких лиц для измерения одного свойства. Случается, что шкала неустойчива потому, что ее пункты произвольно интерпретируются самими исследователями. В особенности это характерно для шкал качественной классификации объектов. В таких (номинальных) шкалах группы объектов классифицируют с помощью описания всех качественных признаков, по которым каждый объект относится к определенному пункту шкалы – классу.
Предположим, что выделено несколько признаков для отнесения определенной деятельности к разряду профессий определенного типа (например, человек-знак). Чтобы выполнить эту операцию однозначно, нужно убедиться, что признаки ясно различимы и при соотнесении видов деятельности с пунктами шкалы не возникает путаницы.
В этом случае объект измеряют одновременно несколько (миниум трое) лаборантов, использующих единую процедуру. Если данные полученные разными лаборантами, высоко согласуются, шкала устойчивая, если нет – неустойчива, и мы начинаем искать другую, более приемлемую размерную величину. Причина неустойчивости шкалы – в плохом отборе индикаторов.
в) Расщепление шкалы. Шкала раздваивается на две половины. Если окажется, что измерения по каждой из них совпадают, их можно рассматривать как равноценные шкалы, суммировать данные и впредь пользоваться одновременно обеими половинами, образующими теперь единую и более надежную шкалу, чем каждая из ее составляющих.
Пример расщепления пункта шкалы:
Первоначальный вариант После расщепления
А. Специальность а1. Считаю свою специальность лучше
очень нравится всех других
а2. Моя специальность одна из лучших
Точность и правильность измерения зависят от (а) степени устойчивости измеряемого объекта или свойства, (б) чувствительности эталона измерения (дробности пунктов шкалы), (в) отсутствия систематических ошибок измерения и, конечно, (г) от устойчивости измерения.
Дробность методики – чувствительность шкалы – прямо связана с точностью измерения.
Шкалы в 10 делений измеряет точнее, чем в 5 или 3 деления. Но дробность пунктов шкалы нельзя увеличивать беспредельно. Надо установить оптимум, удовлетворяющий двум требованиям: максимум градаций шкалы при условии высокой устойчивости результатов измерения. Постепенно повышая дробность эталона измерения и параллельно проверяя шкалу на устойчивость, мы найдем границу, за пределами которой дальнейшее повышение дробности влечет понижение устойчивости измеряемого свойства.
Таким образом, достижение устойчивых данных при максимальной дробности метрики повышает точность измерения. Оно будет удовлетворительно точным, если абсолютная ошибка измерения не превышает 0,5 деления шкалы. Вместе с тем, если ошибка вообще отсутствует, то не исключено что шкала обладает заниженной чувствительностью (особенно в случаях, когда мы предполагаем достаточную вариабельность измеряемого свойства).
Но измерение может быть вполне точным и, вместе с тем, неправильным, постоянно воспроизводя какую-то систематическую ошибку, как это случается с испорченным термометром, в котором ртутный столбик изначально был фиксирован на неверной исходной отметке и постоянно завышает температуру, скажем, на 0,8 градусов.
При квантификации психологических характеристик проблема правильности, т.е. отсутствия уклонений от истинного значения измеряемого свойства, намного сложнее, ибо часто мы в принципе не способны установить, каковы же истинные значения измеряемых свойств (скажем, ценностных ориентаций).
Одна из возможных систематических ошибок – отсутствие “разброса” информации по шкале вследствие того, что какие-то ее пункты “не работают”, т.е. не реагируют на определенное состояние измеряемого свойства. Например, при опросе все ответы концентрируются в позитивном или только в негативном полюсе шкалы.
Другой причиной неправильности может быть плохая различительная способность соседних пунктов шкалы высокой дробности (состоящей, к примеру, из 20 и более градаций).
Date: 2015-10-18; view: 1938; Нарушение авторских прав