Добротность объемного резонатора

Добротность определяется как отношение энергии, запасенной в резонаторе , к энергии потерь в нем за период колебаний . Выражая последнюю через мощность потерь за период Т: , получаем:

(9.9)

Энергия, запасенная в объеме резонатора любого типа

(9.10)

Мощность потерь включает мощность потерь в диэлектрике , заполняющего объем, и мощность потерь в металлических стенках резонатора. При этом выражение (9.9) можно переписать в виде:

(9.11)

или

, (9.12)

где - добротность за счет потерь в диэлектрике;

- добротность за счет потерь в металле.

Мощность потерь в металлических стенках рассчитывается по соотношению

(9.13)

Мощность потерь в диэлектрике с учетом проводимости диэлектрика

(9.14)

С учетом (9.13) и (9.14), выражения для добротностей представимы в виде

(9.15)

(9.16)

Как следует из (9.16), добротность диэлектрика не зависит от формы, размеров и типа колебаний резонатора и полностью определяется тангенсом угла потерь заполняющего его диэлектрика.

Для всех практически значимых типов объемных резонаторов в справочной литературе приведены формулы для расчета добротности. Для прямоугольного резонатора с колебаниями типа и, что-то же самое, , выражение для добротности имеет вид

(9.17)

Приведенные выражения описывают так называемую ненагруженную, или собственную, добротность резонатора. Величина добротность, учитывающая шунтирующее действие внешних цепей, называется нагруженной и описывается как

(9.18)

Здесь - средняя мощность, отдаваемая резонатором во внешнюю цепь, пропорциональная коэффициенту связи ее с резонатором.

10. Элементарные излучатели

Тема занятия. Возбуждение электромагнитных волн в свободном пространстве элементарными излучателями. Рассматриваются задачи определения полей, построения диаграмм направленности, расчету мощности и сопротивления излучения элементарных излучателей.

Решение задачи возбуждения электромагнитных полей в любой точке пространства известными сторонними токами, сводится к решению неоднородной системы уравнений Максвелла, которая имеет вид:

(10.1)

где - плотность стороннего электрического тока с известной функцией пространственного распределения.

При этом определению подлежат все шесть векторных полей Е и Н. Для упрощения поиска решения этого класса задач используются вспомогательные функции, получившие название потенциалов электромагнитного поля, которые, в свою очередь, непосредственно связаны со всеми составляющими поля.

В задачах возбуждения поля электрическими сторонними токами используется электрический векторный и скалярный потенциалы, связанные с векторами поля и выражениями перехода:

(10.2)

где потенциалы и связаны соотношением (удовлетворяют требованиям калибровки):

(10.3)

С учетом последнего неоднородное уравнение Гельмгольца записывается с помощью векторного электрического потенциала

(10.4)

а выражения перехода (10.2) принимают вид

(10.5)

Решение неоднородного уравнения Гельмгольца в интегральном виде дает значение векторного потенциала в точке пространства, отстоящего от области возбуждающих токов 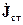на расстоянии

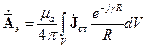(10.6)

Date: 2015-10-18; view: 1023; Нарушение авторских прав