Граничные условия Леонтовича

Кафедра персональной электроники

Г. П. Раевский

МЕТОДИЧЕСКОЕ ПОСОБИЕ

К практикуму

По курсу

ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА И АНТЕННЫ

1. Элементы векторного анализа

Тема занятия Элементы векторного анализа, используемые при расчете электромагнитных полей.

Электромагнитное поле характеризуется силами, действующими на электрические заряды. Поскольку сила – векторная величина, для математического описания ЭМ полей используется аппарат векторного анализа. С его помощью проводится математическое моделирование ЭМ полей, как скалярных, так и векторных [1].

Графически векторное поле может быть представлено в виде набора их силовых линий. В каждой точке силовой линии вектор поля касателен к ней.

Уравнение линии вектора А записывается в виде векторного произведения:

или (1.1)

Ниже приведены основные операции векторного анализа для прямоугольной (декартовой) системы координат.

………………………………………………………………….

Дифференциальные операция со скалярными и векторными полями удобно записывать с помощью символического векторного оператора Гамильтона . Символическое умножение на него скалярной или векторной функции означает дифференцирование по координатным составляющим. В декартовой системе координат оператор Гамильтона записывается как

(1.5)

С его помощью основные операции векторного анализа записываются как:

- умножение вектора на скалярную величину,

- скалярное произведение двух векторов,

- векторное произведение двух векторов.

Дифференциальные векторные операции второго порядка записываются с помощью оператора - так называемого Набла квадрат. В декартовой системе координат этот символический оператор второго порядка записывается как

(1.6)

2. Основные ЗАКОНЫ электромагнЕТИЗМА

Тема занятия. Основные законы электромагнетизма. Уравнения Максвелла. Граничные условия.

Классическая теория электромагнитного поля базируется на уравнениях Максвелла, сформированных им на основе имевшихся к тому времени данных многочисленных экспериментальных исследований электрических и магнитных явлений.

Система уравнений Максвелла в интегральной форме:

(2.1)

В дифференциальной форме:

(2.2)

К основным уравнениям электромагнитного поля относится также уравнение непрерывности тока:

в интегральной форме:

, 2.3)

в дифференциальной форме:

(2.4)

Принятые обозначения:

- вектор напряженности электрического поля, В/м;

- вектор напряженности магнитного поля, А/м;

- вектор электрического смещения (электрической индукции), Кл/м²;

- вектор магнитной индукции, Тл;

- удельная проводимость вещества, См/м;

- объемная плотность электрического заряда, Кл/м³;

- вектор плотности стороннего электрического тока, А/м².

Правая часть первого уравнения Максвелла есть сумма токов различной природы. Выражение

, (2.5)

определяет сумму плотности тока смещения и поляризационного тока .

Плотность тока проводимости определяется как

.

Материальные уравнения для электрического и магнитного полей:

(2.6)

- определяют соотношения между векторами индукции и напряженности поля через абсолютные проницаемости сред, диэлектрическую 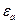и магнитную .

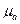На практике обычно пользуется значением относительной (безразмерной величины) проницаемости среды: диэлектрической - , и магнитной - . При этом

Ф/м, Гн/м.

Проницаемости сред могут быть функциями координат (неоднородные среды), зависеть от частоты колебания поля (дисперсионная зависимость) и от величины поля (нелинейные среды). Если параметры среды не зависят от поляризации поля, то среда является изотропной, если зависят – анизотропной.

Для определения значений поля (например, ) на границе двух сред его представляют в виде суммы двух составляющих: - нормальной (перпендикулярной) границе раздела и - тангенциальной (касательной) ей.

Для нормальных составляющих справедливы соотношения:

(2.7)

при отсутствии поверхностных электрических зарядов.

Если на границе раздела сред равномерно распределен электрический поверхностный заряд с удельной плотностью , то

(2.8)

Для тангенциальных составляющих электрического поля справедливо

(2.9)

Если вторая среда – идеальный проводник (с бесконечной проводимостью), то E_1τ=0 и на границе существует только нормальная составляющая электрического поля.

Для магнитной составляющей в общем случае

, (2.10)

На поверхности идеального проводника вводится понятие поверхностного электрического тока , измеряемого в А/м:

, (2.11)

численно равного нормальной составляющей вектора поля на границе и ориентированного перпендикулярно ему.

3. Уравнения Максвелла для гармонических колебаний. ЭнергИЯ электромагнитного поля

Тема занятия. Методы расчета полей и энергетических характеристик для случая гармонических колебаний. Проводится решение уравнений Максвелла в комплексных амплитудах, рассматривается теорема Пойнтинга.

Любой сложный колебательный процесс с помощью метода интеграла Фурье можно представить в виде набора гармонических колебаний. Для колебаний, изменяющихся во времени по гармоническому закону с частотой ω =2π f, при решении прикладных задач используется метод комплексных амплитуд.

В общем случае вектор поля (например, электрического) записывается в виде:

, (3.1)

где в круглых скобках представлен вектор комплексной амплитуды Ė. Дифференцируя по времени уравнения ( 2.2), получаем

(3.2)

Для характеристики диэлектрических сред вводится понятие комплексной диэлектрической проницаемости:

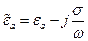, (3.3)

где действительная часть характеризует интенсивность поляризационных свойств материала, а мнимая – плотность токов проводимости.

Потери в диэлектрике за счет токов проводимости принято характеризовать величиной δ угла наклона к действительной оси на комплексной плоскости или значением =σ/ωε_a. В диапазоне СВЧ хорошим считается диэлектрик с <10^-3.

Энергетические соотношения в электромагнитном поле характеризуются теоремой Пойнтинга. Энергия поля, заключенного внутри некоторого объема V, изменяется во времени вследствие:

- превращения части энергии в другие виды энергии, в частности, в тепловую, связанную с протеканием токов проводимости;

- работу сторонних источников, способных как увеличить, так и уменьшить ее запас в заданном объеме V;

- обмена энергией между V и окружающим пространством за счет излучения.

Интенсивность излучения через поверхность S объема V характеризуется величиной, называемой вектором Пойнтинга. Онравен плотности потока энергии излучения и определяется как векторное произведение мгновенных значений полей Е (t) и H (t) в данной точке пространства:

(3.4)

Теорема Пойнтинга определяет баланс энергии области поля внутри области объема V:

. (3.5)

где - мгновенная мощность потерь за счет проводимости;

- мгновенная мощность, привносимая сторонними токами;

- суммарная мгновенная мощность электрического и магнитного полей в объеме V.

В случае гармонических колебаний теорема Пойнтинга в комплексных амплитудах отражает закон сохранения для мощностей, усредненных за период колебания Т.

Действительное (среднее) значение вектора Пойнтинга определяется как:

(3.6)

4. Плоские электромагнитные волны

Тема занятия. Распространение плоской однородной линейно поляризованной ЭМ волны в безграничных средах.

Волновой процесс – явление переноса энергии поля в пространстве и во времени. Для гармонически меняющегося поля (например, Е или Н) - описывается уравнением Гельмгольца:

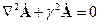(4.1)

Частное решение уравнения Гельмгольца для ЭМ поля, изменяющегося во времени по гармоническому закону в неограниченном пространстве

, (4.2)

где (4.3)

- комплексная постоянная распространения,

- фазовая постоянная, - постоянная затухания.

Знак «минус» в показателе экспоненты указывает, что волна распространяется в положительном направлении оси z (прямая волна), знак «плюс» - в отрицательном (обратная волна).

Плоская волна. С учетом (4.2) и (4.3) общее выражение для мгновенного значения поля прямой плоской ЭМ волны в среде с затуханием:

(4.4)

характеристическим сопротивлением среды.

Аргумент косинуса, т.е. , -фаза волны, функция времени t и пространственной координаты z. Период изменения во времени (при t=const):, , сек, где угловая частота , и в пространстве (при z=const): , 1/м., где λ – длина волны.

Поверхность, удовлетворяющую уравнению , называют волновым фронтом. В данном случае это бесконечная плоскость, перпендикулярная направлению распространения z и перемещающаяся в пространстве со скоростью

, называемой фазовой скоростью.

В плоскости фазового фронта, отношение векторов напряженности электрического и магнитного полей есть величина постоянная, называемая характеристическим сопротивлением среды.

(4.5)

В вакууме , , 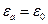. Согласно (4.3), .

м/с, λ₀= С /f, м.

Фазовая скорость ЭМ волны в вакууме равна скорости света С.

Характеристическое сопротивление вакуума Ом - чисто действительная величина. Это означает, что гармонические Е и Н колеблются в фазе.

В среде с произвольными параметрами

, λ=V_ф/f, м

Групповая скорость для узкополосного сигнала определяется как .

Плоская волна переносит энергию в направлении распространения. Для гармонических полей процесс характеризуется вектором Пойнтинга , который иногда удобно записывать через одну из составляющих поля

(4.6)

Через координатные составляющие поле плоской волны определяется как

, ,

где , .

Ориентация вектора зависит от соотношения амплитуд и фаз его координатных составляющих и указывает поляризацию волны. В общем случае конец вектора описывает эллиптическую кривую. При и сдвиге фаз 90⁰ поляризация круговая, при синфазном изменении (наличии одной составляющей) – линейная.

Величина потерь в среде характеризуется постоянной затухания

, 1/м. (4.7)

В радиотехнике затухание принято выражать в децибелах на единицу длины

, дБ/м, (4.8)

связанное с постоянной затухания α соотношением

Величина γ в (4.3), где

,

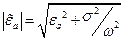определяется как , и

, , (4.9)

В случае постоянные фазы и затухания с достаточной степенью точности рассчитываются по приближенным соотношениям

, (4.10)

5. ЯВЛЕНИЯ на границЕ двух сред.

Тема занятия. Характеристики прошедшей и отраженной волн определяются как функции параметров сред угла падения и поляризации. Рассматриваются приближенные граничные условия Леонтовича.

Зависимость комплексных амплитуд отраженной и преломленной волн от комплексной амплитуды падающей волны определяются через коэффициенты отражения и преломления (прохождения) как

и , (5.1)

полученных с учетом граничных условий (2.9)), (2.10).

В декартовой системе координат плоскость xoy совпадает плоскостью границы раздела сред. Направление падения луча плоской однородной ЭМ волны (направление вектора Пойнтинга) совпадает с плоскостью xoz – плоскостью падения. Углы наклона лучей падающей, отраженной и преломленной волн (φ_пад, φ_{отр и} φ_пр, соответственно) отсчитываются от оси z, перпендикулярной границе раздела сред 1 и 2 (см. рис. 5.1).

Плоскости постоянных фаз с векторами полей и перпендикулярны лучам. Рассматриваются два случая ориентации (линейной поляризации) вектора относительно плоскости падения: параллельно и перпендикулярно плоскости xoz.

Рис.5.1 Падение плоской волны на границу двух сред

под произвольным углом

Явления на границе раздела рассматриваются в предположении, что обе среды без потерь (tgδ =0), а граница раздела – плоская. Тогда соотношения углов падения, отражения и преломления определяются законами Снеллиуса:

(5.2)

Коэффициенты отражения и преломления определяются соотношениями:

при параллельной поляризации

; (5.3)

при перпендикулярной поляризации

,……… ……..(5.4)

где , - характеристические сопротивления сред,

Если волна падает нормально к границе раздела , значения R и T от поляризации не зависят.

При определенном сочетании параметров в средах без потерь отраженная волна может отсутствовать. Угол падения, при котором падающая волна полностью проникает во вторую среду (), называется углом Брюстера . Для случая немагнитных диэлектриков () и при ε₂> ε₁ явление имеет место при параллельной поляризации. При этом

В случае, когда волна падает из воздуха ( =1), .

Если > , то, согласно (5.2), > . Угол падения, при котором = /2, называется углом полного внутреннего отражения , поскольку вся энергия падающей волны отражается от границы раздела коэффициент отражения по модулю тождественно равен единице. При > | R |=1, меняется только фаза. При этом плоскость постоянных фаз волны распространяется вдоль границы раздела сред (вдоль оси x), а плоскость постоянных амплитуд – вдоль оси z. В среде 1 поле вдоль оси z меняется по гармоническому закону – волна становится неоднородной, а в среде 2 - экспоненциально спадает при удалении от границы раздела по закону

,

где - мнимая часть угла преломления при > .

Глубина проникновения поля во вторую среду обратно пропорциональна и и рабочей частоте. Со стороны среды 2 волна как бы прижимается к границе раздела: образуется так называемая поверхностная волна.

Если среда 2 - идеальный металл , то при нормальном падении , согласно граничным условиям, на металле . Поскольку векторы Пойнтинга падающей и отраженной волн равны и противонаправлены,

. (5.5)

При этом вектор плотности поверхностного тока на металле

. (5.6)

численно равен и направлен вдоль вектора .

Граничные условия Леонтовича

Когда среда 2 - неидеальный металл 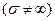, электрическое поле в нем не равно нулю. Относительная комплексная диэлектрическая проницаемость

.

При значениях из (5.1) следует, что угол преломления можно считать равным нулю при любых , т.е. преломленная волна в металлоподобной среде нормальна границе сред (приближение Леонтовича). На границе металла существует отличная от нуля . Несмотря на малость этой величины, она обеспечивает поток вектора Пойнтинга вглубь металла, определяющий тепловые потери. Мощность тепловых потерь определяется как

Полагая, что совпадает по величине с на поверхности идеального металла при , в соответствии с (5.5), .

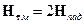6. Полый металлический волновод

Тема занятия. На примере явлений в системе двух параллельных металлических пластин рассматриваются основные характеристики волн в направляющих металлических структурах. Проводится анализ полей, характеристик распространения и затухания типов волн и распределение токов проводимости в стенках прямоугольных металлических волноводов. Рассматриваются способы эффективного возбуждения различных типов волн.

Date: 2015-10-18; view: 1324; Нарушение авторских прав