Оценка точности уравнения регрессии

Как уже отмечалось, оценки параметров уравнения регрессии

вычисляются по выборочным данным и лишь приближённо равны этим параметрам. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности. При решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов отклонений зависимой переменной: на две составляющие, источниками которых являются отклонения за счёт регрессионной зависимости (SSR) и за счёт случайных ошибок (SSE), причём

Из теории статистики известно, что SST = SSR + SSE или

Аналогичное разложение имеет место и для числа степеней свободы соответствующих сумм:

df_T = df_R + df_E,

где df_T = n – 1 – общее число степеней свободы;

df_R = m – число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);

df_E = n – m – 1 – число степеней свободы, соответствующее ошибкам.

Разделив соответствующие суммы квадратов на степени свободы, получим средние квадраты или дисперсии, которые сравниваются по критерию Фишера для проверки гипотезы о равенстве нулю одновременно всех коэффициентов регрессии против альтернативной: не все коэффициенты регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что уравнение регрессии значимо, в противном случае оно ничего не отражает и не может быть использовано в анализе.

Итак, процедура дисперсионного анализа регрессии состоит в следующем:

рассчитываются суммы квадратов SSR и SSE;

определяются средние квадраты или дисперсии, соответствующие регрессии и ошибкам: MSR = SSR / m и MSE = SSE / n – m – 1;

сравниваются полученные дисперсии на основе критерия Фишера, причём MSR ³ MSE, следовательно если F _/2,m,n-m-1 > F, то уравнение регрессии значимо (не все коэффициенты уравнения регрессии равны нулю), в противном случае – не значимо.

Дисперсионный анализ регрессии удобно проводить в таблице вида:

Таблица 9.1 – Таблица дисперсионного анализа регрессии

Источник	Сумма квадратов	Степени свободы	Средние квадраты	F-отношение
Модель ошибки	SSR SSE	m n – m – 1	MSR MSE	F=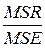
Общая	SST	n – 1

Вернёмся к MSE. Это тоже характеристика точности уравнения регрессии. Этот показатель особого самостоятельного значения не имеет, но участвует в вычислении других показателях точности. Например, корень квадратный из MSE называется стандартной ошибкой оценки по регрессии (S_y,x) и показывает, какую ошибку в среднем получим, если значение зависимой переменной оценивать по уравнению регрессии:

Кроме того, этот показатель в неявном виде участвует в определении коэффициента множественной детерминации (R²):

или после преобразований:

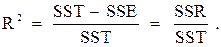
Отсюда следует, что коэффициент множественной детерминации отражает долю вариации изучаемого (результирующего) показателя, обусловленную вариацией за счёт регрессионной зависимости. Коэффициент множественной детерминации иногда выражают в процентах, поэтому, например, если R² = 75%, то это означает, что изменение зависимой переменной на 75% объясняется изменением включённых в уравнение регрессии независимых переменных, а остальные 25% – это изменения за счёт неучтённых факторов и случайных отклонений (ошибок).

Корень квадратный из коэффициента множественной детерминации называется коэффициентом множественной корреляции:

который показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными.

Ясно что, R² и R изменяются от нуля до единицы и равны единице, если SSE = 0, т.е. связь линейная функциональная и равны нулю, если SST = SSE, т.е. связь отсутствует.

Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:

с m числом степеней свободы числителя и n – m – 1 – знаменателя.

В социально-экономических исследованиях встречается преобразованная формула определения R², имеющая вид:

или в других обозначениях:

,

где S_y,x² – выборочная остаточная дисперсия независимого показателя;

S_y² – его общая выборочная дисперсия.

Как уже отмечалось, – стандартная ошибка оценки по регрессии.

Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо ни были они связаны с независимой переменной. Следуя этой логике, для увеличения точности отражения изучаемой зависимости в уравнение регрессии может быть включено неоправдано много независимых переменных. Точность модели при этом увеличится незначимо, а размерность модели возрастёт так, что её анализ будет затруднён. Кроме того, качество оценок при этом ухудшается. Для исключения такого недостатка рассматривают исправленный (на число степеней свободы) коэффициент множественной детерминации:

Этот коэффициент позволяет избежать переоценки независимой переменной при включении её в уравнение регрессии. Если добавление переменной приводит к увеличению 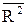, то включение её в уравнение регрессии оправдано, в противном случае – нет. Исправленный коэффициент детерминации всегда меньше неисправленного и является несмещённой оценкой для коэффициента множественной детерминации, в то время как неисправленный – завышенный, смещённой оценкой.

Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты уравнения регрессии равны нулю, против альтернативной – не все коэффициенты регрессии равны нулю. В последнем случае, т.е. если нулевая гипотеза отклонена, встаёт вопрос: какие из коэффициентов равны нулю, а какие значимо отличны от нуля?

Date: 2015-10-18; view: 2363; Нарушение авторских прав