Задача анализа матрицы парных коэффициентов корреляции

Корреляционный и регрессионный анализы настолько тесно связаны,

что, как правило, редко рассматриваются отдельно друг от друга. Если в корреляционном анализе выявляется наличие и теснота связи, то в регрессионном – конкретный вид такой связи. Одно из различий этих двух видов анализа заключается в том, что в корреляционном анализе переменные равноправны, а в регрессионном анализе они делятся на зависимые и независимые. Такое деление в последнем случае хотя и обязательно, но довольно условно. Осуществляется это исходя из профессионально-логических соображений, и его результат зачастую зависит от цели исследования. Эта терминология не совсем удачно отражает суть дела, и означает лишь то, что в регрессионном анализе значение зависимой переменной восстанавливается по известным значениям независимых переменных. На самом же деле независимые переменные зачастую зависят, в том числе и друг от друга.

Идеальным условием реализации регрессионного анализа является независимость независимых переменных между собой. Ясно, что это практически не выполняется, но совсем уж нежелательно, чтобы между независимыми переменными наблюдалась тесная корреляционная взаимосвязь. В этом случае говорят о коллинеарности переменных. Считается, что две случайные переменные коллинеарны, если коэффициент корреляции между ними не менее 0,8. Если таких переменных несколько, то говорят о мультиколлинеарности. Как уже отмечалось, мультиколлинеарность – нежелательное явление в регрессионном анализе, и её выявление является одной из задач анализа матрицы парных коэффициентов корреляции.

Матрица парных коэффициентов корреляции получается, если для набора переменных y, x₁, x₂,..., x_m рассчитать парные коэффициенты корреляции и разместить их в виде матрицы. В дальнейшем переменную y будем называть зависимой, а остальные – независимыми. И хотя для корреляционного анализа они равноправны, в целях дальнейшего использования мы их будем различать. Поскольку r_xy = r_yx, корреляционная матрица симметрична относительно своей главной диагонали, на которой проставлены единицы, поэтому обычно анализируют одну из частей корреляционной матрицы (верхнюю или нижнюю относительно главной диагонали). Пусть корреляционная матрица R имеет вид:

y x₁ x₂ x_m

.

Договоримся анализировать верхнюю часть матрицы. Тогда первая строка матрицы содержит коэффициенты корреляции между зависимой переменной y и независимыми переменными х₁, х₂, …, x_m. Анализируют эти коэффициенты с целью выявления значимых и незначимых независимых переменных. Значимость переменной здесь понимается с точки зрения влияния её на зависимую переменную. Если проверка гипотезы Н₀: 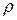= 0 покажет, что коэффициент корреляции незначимо отличен от нуля, то это означает, что соответствующая независимая переменная не значимо влияет на зависимую переменную, т.е. незначима и в уравнение регрессии её включать не следует. Отметим, что подобные выводы правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чём речь впереди.

Второй этап анализа матрицы парных коэффициентов корреляции – выявление мультиколлинеарности среди независимых переменных. Для этого просматривается оставшаяся часть матрицы R (кроме первой строки) и выделяют коэффициенты, по величине ³ 0,8. Они и укажут на коллинеарные переменные. Обычно в уравнение рагрессии не включают те из них, которые слабее связаны с зависимой переменной.

Date: 2015-10-18; view: 654; Нарушение авторских прав