Свойства двойственных оценок для различных критериев оптимальности

Рассмотрим экономический смысл двойственных оценок (оценок оптимального плана) на примере экономико-математической задачи наилучшего использования ресурсов (в частности, фонда времени работы производственного оборудования), формулируемой с разными критериями оптимальности: максимум прибыли (вариант Р), минимум себестоимости (вариант С) и максимум выпуска продукции в заданном ассортиментном соотношении (вариант А).

Рассмотрим последовательно формулировки прямых и двойственных задач для вариантов Р, С и А и проанализируем экономические свойства двойственных оценок в каждом случае.

Введём обозначения:

– (станко-час/шт.) – норма затрат станочного времени по группе оборудования i на изготовление продукции j по технологическому способу s;

b_i (станко-час) – располагаемый фонд станочного времени по группе оборудования i;

x_j^s (шт.) – интенсивность способа s, с помощью которого производится продукция j;

p_j^s (руб./шт.) – прибыль от реализации единицы продукции j по способу s;

М_j (шт.) – производственная программа выпуска j-й продукции;

C_j^s (руб./шт.) – себестоимость единицы продукции j, производимой по способу s.

Задача на максимум прибыли (max P)

Прямая задача Двойственная задача

; (4.14) ; (4.14а)

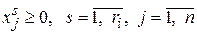; (4.15) ; (4.15а)

; (4.16) . (4.16а)

Задача на минимум себестоимости (min С)

Прямая задача Двойственная задача

; (4.17) ; (4.17а)

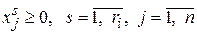; (4.18) ; (4.18а)

; (4.19) 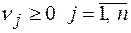; (4.19а)

; (4.20) . (4.20а)

Задача на максимум выпуска продукции (max A)

Прямая задача Двойственная задача

; (4.21) ; (4.21а)

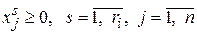; (4.22) ; (4.22а)

; (4.23) 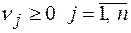; (4.23а)

; (4.24) 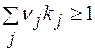; (4.24а); (4.25) . (4.25а)

Введём дополнительные обозначения:

k₁ (шт./компл.) – количество продукции вида j в одном комплекте;

Z (компл.) – общее количество выпускаемых комплектов.

На основе этих обозначений условие (4.23) 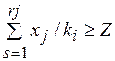означает условие комплектности.

Обозначим через u_i оценку i-гo ресурса (т.е. времени работы i-й группы оборудования) и через v_j – оценку j-гo вида продукции.

Единицы измерения оценок в варианте Р определяются на основе соотношения (4.15а). Исходя из единиц измерения прямой задачи Р_j (руб./шт.) и (станко-час./шт.) будем иметь следующие единицы измерения оценок: u_i (руб./станко-час). Это определённого вида прибыль (в руб.), приходящаяся на один станко-час работы i-й группы оборудования. В связи с отсутствием ограничений по выпуску продукции в варианте Р не будет оценок продукции.

В варианте С единицы измерения оценок также определяются исходя из основных ограничений двойственной задачи (4.18а). Из С_j^s (руб./шт.) вытекает, что v_j (руб./шт.) – себестоимость (затраты определённого типа) в рублях на единицу продукции, с учётом же смысла показателей а_ij^s (станко-час/шт.) оценка оборудования будет u_i (руб./станко-час), что также представляет собой определённым образом преобразованную часть себестоимости продукции, отнесённую к группе оборудования i.

В варианте А единица измерения оценок определяется исходя из
соотношения (4.24а) и (4.22а). Из соотношения (4.24а) оценка
продукции v_j (компл./шт.) показывает определённым образом оценённую
связь между общим выпуском продукции (в комплектах) и выпуском
продукции j (в шт.). На основе соотношений (4.22) определяется единица измерения оценок оборудования u_i (компл./станко-час), непосредственно характеризующих связь между выпуском продукции в комплектах и затратами станочного времени по i-й группе оборудования (в станко-час).

Перейдём теперь к рассмотрению конкретных экономических свойств оценок оптимального плана.

Свойство 1. Оценки как мера влияния ограничений на оптимальное значение целевой функции.

В задаче Р оценка u_i^* (руб./станко-час) показывает прирост совокупной прибыли от реализации продукции при увеличении фонда времени работы оборудования на единицу (при бесконечно малом увеличении).

В задаче С u_i^* (руб./станко-час) характеризует экономию (прирост) совокупных затрат на выпуск продукции при увеличении (уменьшении) фонда времени работы оборудования группы i на единицу. Соответственно (руб./шт.) характеризует прирост (снижение) совокупных затрат при увеличении (уменьшении) производственной программы по продукции j на одну единицу.

Аналогично в задаче А оценка u_i (компл./станко-час) 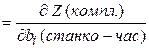показывает прирост (сокращение) выпуска комплектной продукции при соответствующем бесконечно малом изменении фонда времени работы оборудования b_i.

Примечание. В данной постановке оценка v_j (компл./шт.) не имеет содержательной интерпретации с точки зрения свойства 1, но если несколько переформулировать задачу (разделить обе части 4.23 на Z и умножить на k_j), можно получить нелинейную оценку W_j (компл./шт.), которая покажет, как изменение количества продукции в комплекте (т.е. величины k,) повлияет на изменение общего выпуска

Значение свойства 2 состоит в том, что оно позволяет выявить направления мероприятий по расшивке узких мест, обеспечивающих получение наибольшего экономического эффекта, а также целесообразные изменения в структуре выпуска продукции с позиций общего оптимума.

Точной мерой влияния ограничения на целевую функцию оценка является лишь при бесконечно малом приращении ограничения. Оценки выполняют эту функцию в достаточно широких пределах своей устойчивости.

Как известно, оценки не меняют своей величины, если не меняется набор базисных переменных в оптимальном плане, тогда как значения этих переменных в плане могут изменяться.

Ослабление какого-либо i-гo ограничения приводит к тому, что с определённого момента оказывается возможным изменить структуру (набор переменных) в базисе плана и это приводит к скачкообразному уменьшению величины оценки. Так продолжается до тех пор, пока i-й ресурс вообще перестает быть дефицитным и оценка обращается в нуль. Характер изменения оценки иллюстрирует рисунок 4.1.

Рисунок 4.1 – Иллюстрация изменения оценки

На рисунке b_i⁽⁰⁾ – начальный лимит i-гo ресурса, которому в оптимальном плане соответствует оценка u_i⁽⁰⁾ > 0. В пределах [b_i⁽⁰⁾, b_i⁽¹⁾] базис оптимального плана, а следовательно, и значения u_i⁽⁰⁾ остаются неизменными. Мероприятия по изменению лимита ресурсов в этих пределах носят название малых мероприятий, их эффективность может быть точно измерена с помощью оценок. Однако при изменении лимита до величины, превышающей b_i⁽¹⁾, оценка уменьшается вследствие существенного уменьшения дефицитности i-гo ресурса, и эффект от такого мероприятия, которое выходит за пределы устойчивости оценки u_i и относится к категории больших мероприятий, может быть подсчитан лишь с помощью значений u_i⁽⁰⁾ и u_i⁽¹⁾. Соответственно при превышении величины b_i⁽²⁾ ресурс становится недефицитным, его оценка обращается в нуль: u_i⁽²⁾ = 0.

Таким образом, для малых мероприятий двойственные оценки являются точной мерой влияния ограничений на значение целевой функции, а точность определения влияния на оптимум больших мероприятий зависит от точности прогноза изменения оценки по мере уменьшения дефицитности i-гo ресурса.

Свойство 2. Оценки как мера дефицитности ресурсов и продукции. Это свойство оценок вытекает из второй теоремы двойственности. Так как для пары сопряжённых условий оптимального плана одно условие выполняется как строгое равенство, а другое – как строгое неравенство, то во всех трёх задачах дефицитный ресурс полностью используется в оптимальном плане (где ), имеет положительную оценку Uu* > 0, а недефицитный, не полностью используемый ресурс (для которого ) имеет нулевую оценку u_i* = 0. Аналогично в задачах С и А продукция, которая производится в минимально необходимом количестве (условия (4.19) и (4.23) обращаются в равенства), получает положительную оценку v_j* > 0, а не эффективная продукция, которая при заданных ресурсах может быть произведена сверх необходимого количества (условия (4.19) и (4.23) обращаются в неравенства), получает оценку V_j* = 0.

В задаче Р величина u_i (руб./станко-час) – это прокатная оценка оборудования. Она характеризует ограниченность фонда времени работы оборудования i, что не позволяет использовать i-e оборудование по всем без исключения направлениям, где оно может дать положительный эффект. Из-за этого приходится использовать оборудование i лишь при тех технологических способах, которые в результате решения задачи признаны наиболее эффективными с позиции общего оптимума. В результате такого рода «задалживания» оборудования в одних способах «недополучается» прибыль в других способах из-за использования менее эффективных ресурсов.

Оценка u_i (руб./шт.) как раз и показывает ту граничную (предельную) величину прибыли, недополученную вследствие дефицитности фонда времени работы i-й группы оборудования, которая в случае загрузки i-й группы в оптимальном плане должна быть компенсирована дополнительно получаемой прибылью. Чем выше величина оценки u_i, тем острее дефицитность i-гo ресурса. Естественно, для недефицитного, не полностью загруженного оборудования u_i* (руб./станко-час) = 0.

В задаче С u_i (руб./станко-час) также прокатная оценка оборудования, но она показывает величину «несэкономленной» себестоимости при использовании тех технологических способов, где не применяется оборудование вида i из-за «задалживания» этого оборудования при работе по другим способам.

Оценка продукции v_j (руб./шт.) показывает, какую часть совокупных затрат на выполнение всей производственной программы экономически оправдано относить на продукцию вида j. Если какая-либо продукция производится как побочный результат деятельности, её оценка v_j* = 0 и дополнительные усилия на её производство не являются оправданными.

В задаче А оценка u_i (компл./станко-час) показывает, какова предельная величина недополученного выпуска продукции в заданном ассортименте (в комплектах) из-за «задалживания» дефицитного фонда времени работы оборудования i. Там, где имеется такое «задалживание», оно должно быть компенсировано дополнительным выпуском продукции.

Оценка продукции v_j (компл./шт.) характеризует ту часть общего выпуска продукции j в комплектах, которую можно рассматривать как вклад в достижение общей цели. Эта величина для сопутствующей (побочной) продукции также равна нулю.

Таким образом, оценки u_i и v_j – это количественно новые показатели, экономически связывающие расход ресурса и выпуск продукции в отдельных звеньях системы (технологических способах) с общей целью системы и чётко реагирующие на степень ограниченности (дефицитности) продукции и ресурсов.

Свойство 3. Оценки как инструмент определения эффективности отдельных вариантов, технологических способов с позиций общего оптимума.

Это свойство оценок вытекает из второй теоремы двойственности при применении её к соотношениям (4.10) – (4.11).

В оптимальной задаче Р может быть включён лишь тот способ, для которого прибыль, недополученная из-за «задалживания» в этом способе дефицитного оборудования , покрывается полученной прибылью p_j^s. Соответственно там, где такое покрытие не обеспечено, технологический способ не может быть включён в оптимальный план.

В задаче С общая оценка варианта, включаемого в оптимальный план, имеет вид

.

В правой части этого соотношения указана сумма прямых затрат c_j^s на продукцию j при производстве её способом s и затрат системы, возникающих из-за «задалживания» в способе дефицитных ресурсов (), которые называются затратами обратной связи. Такого рода сумма, называемая дифференциальными затратами, показывает, какую часть совокупных затрат всей системы следует в построенном оптимальном плане относить на продукцию j, производимую способом s. Эта величина полных дифференциальных затрат на продукцию (j, s) сравнивается с оценкой v_j* – величиной экономически оправданных затрат на производство продукции j. В оптимальный план включаются те способы, для которых полные дифференциальные затраты совпадают с оценкой экономически оправданных затрат, и не включаются способы, для которых дифференциальные затраты превышают их экономически обоснованную величину.

Для задачи А сравнивается величина эффекта v_j* (выпуск комплектов), который в оптимальном плане может быть отнесён непосредственно на продукцию j, с той суммой эффекта , который недополучен вследствие «задалживания» дефицитного оборудования при работе по данному способу. В оптимальный план включаются способы, где полученный эффект покрывает недополученный. И наоборот, способы, где потенциальные потери при выпуске комплектной продукции из-за отвлечения из системы лучших ресурсов превышают возможный экономический эффект, не включаются в план.

Свойство 4. Оценки как инструмент балансирования суммарных затрат и результатов.

Это свойство вытекает из условия (4.7) теоремы 1 и позволяет в целом сопоставить и сбалансировать затраты и результаты экономической системы. При этом как затраты, так и результаты оцениваются с позиций концепции оптимального планирования с помощью соответствующих показателей. Исходя из этой концепции в широком смысле под результатом понимается вклад в достижение обшей цели системы, а под затратами – упущенные возможности достижения этой цели.

В конкретных задачах такого рода соотношение «затраты – результаты» в точке оптимума (равновесие затрат и результатов) имеет различное экономическое содержание.

В задаче Р смысл равенства (4.7) состоит в том, что максимум прибыли может быть обеспечен лишь при минимуме недополученной прибыли от использования дефицитных ресурсов.

В задаче С обеспечение минимума затрат (Z_min) связано с максимизацией чистого эффекта от использования ресурсов (W_max), т.е. превышением суммарной оценки производимой продукции над суммарной оценкой затрат, возникающим в связи с распределением дефицитных ресурсов.

В задаче А максимум выпуска комплектной продукции может быть обеспечен лишь при минимуме неиспользованных резервов, что выражается в минимальном уровне недополучаемого выпуска при распределении дефицитных ресурсов.

Date: 2015-10-18; view: 1810; Нарушение авторских прав