Анализ чувствительности модели

В большинстве случаев принятия решений полезно составить предварительный план действий, чтобы проанализировать, какое воздействие на принятое решение окажут изменения, вносимые в исходную задачу. Большое значение в линейном программировании имеет анализ чувствительности модели. Этот метод позволяет учесть:

– воздействие дополнительного количества лимитирующего ресурса;

– воздействие дополнительного количества нелимитирующего ресурса;

– воздействие изменений в коэффициентах целевой функции.

Итоговая симплексная таблица при решении задачи линейного программирования содержит оптимальное значение целевой функции, значения основных и балансовых переменных. Последние, как известно, соответствуют остаткам ресурсов. Кроме того, в ней указываются оценки (теневые цены) ресурсов. Информацию итоговой таблицы симплексного метода можно использовать также в анализе чувствительности модели, чтобы выявить общее воздействие изменений в запасах лимитирующих ресурсов и в коэффициентах целевой функции на значение целевой функции.

При определении интервалов изменения коэффициентов целевой функции необходимо вычислить пределы увеличения и уменьшения этих коэффициентов по формулам

для d_pi < 0;

для d_pi > 0,

где y_i* – двойственные оценки в оптимальном решении (элементы Z – строки итоговой симплексной таблицы);

d_pi – элементы строки, соответствующей р-й базисной переменной в итоговой симплексной таблице.

Интервал изменения коэффициента С_р при переменной х_р в целевой функции имеет вид

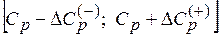. (4.12)

Если изменение коэффициента С_р находится в интервале (4.12), то состав базисных переменных и их значения в оптимальном плане не изменятся. Если же изменение С_р не входит в интервал изменения (4.12), то в оптимальном плане изменятся и состав базисных переменных и их значения.

В случае если переменная х_k не входит в базис оптимального решения, то интервал изменения коэффициента С_k будет

[0; С_k + у_k* ],

где у_k* – оценка балансовой переменной х_k в оптимальном плане (находится в Z-строке), показывающая превышение оценки затрат ресурсов над ценой единицы k-й продукции.

Аналогично находятся границы изменения правых частей ограничений

(4.13)

где

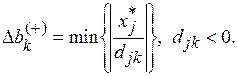
Здесь x_j* – значения базисных переменных в оптимальном решении исходной задачи.

Если изменения правых частей ограничений не выйдут за пределы интервала (4.13), то структура базисных переменных окажется той же, что и в оптимальном решении, а их значения изменятся. При этом оценки оптимального плана (значения y_i^* в Z-строке) не изменятся и их можно использовать для оценки изменённой целевой функции.

Date: 2015-10-18; view: 424; Нарушение авторских прав