Угол между прямыми на плоскости

Пусть на плоскости заданы декартова система координат и две прямые l₁ и l₂ с уравнениями A_i×x+B_i×y+C_i = 0 (i = 1, 2).

Если эти прямые пересекаются в одной точке, то образуется четыре угла (см. рис.), которые разбиваются на две пары равных вертикальных углов j и q и дополняют друг друга до p. Наименьший из этих углов называется углом между прямыми l₁ и l₂ и обозначается Ð (l₁, l₂ ). Ясно, что угол между прямыми всегда не превосходит . Если прямые совпадают или параллельны, то угол между ними считается равным 0.

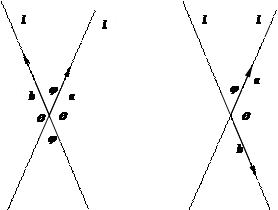1) через направляющие векторы: отложим от точки пересечения направляющие векторы a (–B₁; A₁) и b (–B₂; A₂). Возможны два основных расположения этих векторов (см. рис.). В первом случае Ð (l₁, l₂) = j = Ð( a, b ), а во втором Ð (l₁, l₂) = =j = p–q = p – Ð( a, b ). Таким образом, если Ð( a, b ) £ 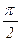(т.е. cos Ð(a, b) ³ 0), то Ð (l₁, l₂) = j = Ð(a, b), cos Ð (l₁, l₂) = +cos Ð(a, b), а если Ð(a, b) > 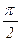(т.е. cos Ð(a, b) < 0), то Ð (l₁, l₂) = p – j = p – Ð(a, b), cos Ð (l₁, l₂) = –cos Ð(a, b). В любом случае cos Ð (l₁, l₂) = = | cos Ð( a, b ) | и, вспоминая связь косинуса угла между векторами со скалярным произведением и его выражением через координаты, получаем Ð (l₁, l₂) = arc cos | cos Ð( a, b ) | = = arc cos 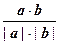= arc cos 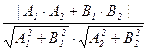. Эта формула работает даже, если прямые совпадают или параллельны. В этом случае векторы a и b коллинеарны, так что величина 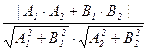равна 1 (проверьте!!!) и Ð (l₁, l₂) = arc cos 1 = 0.

2) через угловые коэффициенты: С понятием угла тесно связано понятие углового коэффициента прямой и уравнение прямой с угловым коэффициентом.

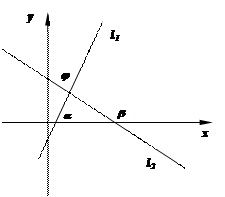
Пусть на плоскости заданы две прямые l₁ и l₂ с уравнениями y = k_i×x+b_i (i = 1, 2). Тог­да, как показывает рисунок (рассмотрите все возможности!!), Ð (l₁, l₂) = j = b – a и

tgj = tg(b–a) = 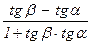= 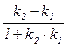и j Î [0; 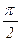]. Таким образом, получаем: Ð (l₁, l₂) = arc tg .

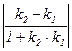Таким образом, доказана

Теорема (о вычислении угла между прямыми). (1) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат общими уравнениями A_i×x+B_i×y+C_i = 0 (i = 1, 2), то выполнено равенство

Ð (l₁, l₂) = arc cos .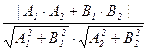

(2) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат уравнениями с угловыми коэффициентами y = k_i×x+b (i = 1, 2), то

Ð (l₁, l₂) = arc tg .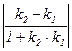

Следствие (о перпендикулярности прямых). (1) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат общими уравнениями A_i×x+B_i×y+C_i = 0 (i = 1, 2), то они перпендикулярны тогда и только тогда, когда A₁×A₂+B₁×B₂ = 0.

(2) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат уравнениями с угловыми коэффициентами y = k_i×x+b (i = 1, 2), то они перпендикулярны тогда и только тогда, когда k₁×k₂ = –1.

Доказательство следует из того, что j = 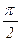Û cos j = 0 Û tg j = +∞.

Date: 2015-10-18; view: 609; Нарушение авторских прав