
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства скалярного произведения
|
|
10. Скалярный квадрат а2 = а × а вектора а равен квадрату длины вектора: а2 = | a |2.
Непосредственно следует из определения: а2 = а × а = | a |×| а |×cos  = | a |2×cos 0 = | a |2 .
= | a |2×cos 0 = | a |2 .
20. Вектор нулевой тогда и только тогда, когда его скалярный квадрат равен нулю: а = 0 Û а2 = 0.
В самом деле, а = 0 Û | a | = 0 Û | a |2 = 0 Û а2 = 0.
30. Скалярное произведение векторов не зависит от порядка перемножаемых векторов: а × b = b × a.
Непосредственно следует из определения: а × b = | a |×| b |×cos 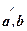 = | b |×| a |×cos
= | b |×| a |×cos  = b × a.
= b × a.
40. Если a (x; y; z) и b (u; v; w) – векторы, координаты которых вычислены относительно некоторой декартовой системы координат, то а × b = x×u+y×v+z×w.
 По теореме косинусов для D АВС (см. рис.) имеем: | b – a |2 = | a |2+| b |2–2| a |×| b |×cos
По теореме косинусов для D АВС (см. рис.) имеем: | b – a |2 = | a |2+| b |2–2| a |×| b |×cos 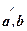 , т.е. a × b =
, т.е. a × b = 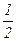 ×{| a |2+| b |2–| b – a |2}. Если бы уже была доказана формула | c | =
×{| a |2+| b |2–| b – a |2}. Если бы уже была доказана формула | c | =  для вычисления длины вектора c (p; q; r) по его декартовым координатам p, q, r, то учтя, что b – a (u–x; v–y; w–z), сразу получили бы
для вычисления длины вектора c (p; q; r) по его декартовым координатам p, q, r, то учтя, что b – a (u–x; v–y; w–z), сразу получили бы
a × b = 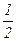 ×{x2+y2+z2+u2+v2+w2– –(u–x)2–(v–y)2–(w–z)2} =
×{x2+y2+z2+u2+v2+w2– –(u–x)2–(v–y)2–(w–z)2} = 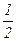 ×{2×(x×u+y×v+z×w)} =x×u+y×v+z×w, что и
×{2×(x×u+y×v+z×w)} =x×u+y×v+z×w, что и
требовалось.
Таким образом, остаётся обосновать использованную формулу для длины вектора в декартовых координатах.
Лемма (о вычислении длины вектора в декартовых координатах). Пусть c (p; q; r) – вектор, координаты которого вычислены в некоторой декартовой системе координат. Тогда | c | =  .
.
 Доказательство. Отложив вектор c =
Доказательство. Отложив вектор c =  от начала координат, получим по теореме Пифагора: | c |2 = OM2 = OM¢ 2+MM¢ 2 = OA¢ 2+OB¢ 2+ MM¢ 2 = (p×OA)2+(q×OB)2+(r×OC)2 = = p2×12+q2×12+r2×12 = p2+q2+r2, что и требовалось. Лемма доказана.
от начала координат, получим по теореме Пифагора: | c |2 = OM2 = OM¢ 2+MM¢ 2 = OA¢ 2+OB¢ 2+ MM¢ 2 = (p×OA)2+(q×OB)2+(r×OC)2 = = p2×12+q2×12+r2×12 = p2+q2+r2, что и требовалось. Лемма доказана.
50. Скалярное произведение векторов линейно по обоим аргументам: ( a + b )× с = a × c + b × c, a ×( b + c ) = a × b + a × c.
В самом деле, записав векторы в координатах a (x; y; z), b (u; v; w), c (p; q; r) в некоторой декартовой системе координат, получим ( a + b )(x+u; y+v; z+w), ( b+c )(u+p; v+q; w+r) и по 40 ( a + b )× с =(x+u)×p+(y+v)×q+(z+w)×r = (x×p+y×q+z×r)+(u×p+v×q+w×r) = a × c + b × c, a ×( b + c ) = x×(u+p)+ +y×(v+q)+z×(w+r) = (x×u+y×v+z×w)+(x×p+y×q+z×r) = a × b + a × c, что и требовалось.
60. Скалярное произведение однородно по обоим аргументам: (l× a )× b = l×( a × b ) = a ×(l× b ).
Следует из определения: например, (l× a )× b = |l× a |×| b |×cos  = |l|×| a |×| b |×sg(l)×cos
= |l|×| a |×| b |×sg(l)×cos 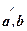 = = l×( a × b ), где sg(l) – знак числа l (почему cos
= = l×( a × b ), где sg(l) – знак числа l (почему cos  = sg(l)×cos
= sg(l)×cos 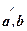 ?!?).
?!?).
70. Если известны декартовы координаты векторов a (x; y; z) и b (u; v; w), то угол между ними можно вычислить по формуле 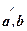 = arccos
= arccos 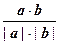 =arc cos
=arc cos  .
.
80. Два вектора a (x; y; z) и b (u; v; w), координаты которых заданы в декартовой системе координат ортогональны тогда и только тогда, когда x×u+y×v+z×w = 0.
Действительно a ^ b Û a × b = 0 Û x×u+y×v+z×w = 0.
 Задача. Докажите, что прямоугольный параллелепипед ABCDA1B1C1D1 является кубом тогда и только тогда, когда углы между его длинная диагональ AC1 образует равные углы с рёбрами АА1, АВ и AD.
Задача. Докажите, что прямоугольный параллелепипед ABCDA1B1C1D1 является кубом тогда и только тогда, когда углы между его длинная диагональ AC1 образует равные углы с рёбрами АА1, АВ и AD.
Решение. Рассмотрим декартову систему координат, начало которой совпадает с вершиной А, а оси направлены по прилегающим к А рёбрам параллелепипеда. Если длины этих рёбер a, b, c, то A(0; 0; 0), B(a; 0; 0), D(0; b; 0), A1(0; 0; c), C1(a; b; c),  (a; b; c), и условия равенства углов с осями записываются в виде равенства косинусов углов между
(a; b; c), и условия равенства углов с осями записываются в виде равенства косинусов углов между  и базисными векторами i, j, k:
и базисными векторами i, j, k:  = =
= =  =
=  . Ясно, что эти равенства равносильны равенству длин всех рёбер параллелепипеда.
. Ясно, что эти равенства равносильны равенству длин всех рёбер параллелепипеда.
МЕТОДИКА 21. «Действия с векторами»
Структура урока:
1. Организационный момент
2. Ознакомление с целью урока
3. Проверка знаний фактического материала (формул, правил, умений)
4. Проверка умений сам-но применять знания в стандартных и измененных условиях
5. Коррекция и проверка
6. Подведение итогов.
Цели:
| Уч. цели | 1 уровень | 2 уровень | 3 уровень | ||
| Знание | Ученик знает | ||||
| Термины: вектор, начало и конец вектора, нулевой вектор, длина (модуль) вектора, коллинеарные векторы, сонаправленные и противоположно направленные векторы, равные векторы, координаты вектора, сложение, вычитание, умножение вектора на число, скалярное и векторное умножение векторов. | Определения понятий сложение, вычитание, умножение вектора на число, скалярное и векторное умножение векторов, преобразование векторных равенств и их замена алгебраическими, разложение вектора по координатам, отыскание величин, связанных с векторами – длин отрезков, углов, правила треугольника, параллелограмма и многоугольника. | Основные понятия и свойства действий с векторами, формулы для суммы, разности векторов, произведения вектора на число, скалярного произведения векторов, доказательство отдельных теорем, обобщенные приемы для вычисления суммы, разности и скалярного произведения векторов, произведение вектора на число | |||
| Понимание | Ученик понимает | ||||
| Узнает и воспроизводит изученные термины, выполняет чертежи к простейшим задачам, краткую запись условий задачи, приводит примеры и выполняет простейшие доказательства. | Интерпретирует словесный и графический материал, используя специальные символы, приводит контрпримеры для коллинеарных векторов, выделяет частные и специальные приемы решения задач на вычисление, доказательство и построение | Преобразует словесный и графический материал в математические выражения и обратно относительно определения векторов и действий с ними, выводит следствия, перестраивает известные и находит новые приемы учебной деятельности | |||
| Умения и навыки | Ученик умеет | ||||
| Решает простейшие задачи на вычисление и доказательство по образцу, используя частные приемы, решает задачи на вычисление неизвестной величины, используя формулу, находит ответы на вопросы по учебнику с помощью учителя | Решает типовые и прикладные задачи в стандартных ситуациях по данным формулам, используя частные приемы решения задач на вычисление, выделяет главное в учебном тексте, самостоятельно отвечает на вопросы, использует дополнительную литературу для образования, составляет задачи по образцу | Решает типовые и прикладные задачи в нестандартных ситуациях, самостоятельно использует обобщенные приемы решения задач, приводит несложные исследования средствами математики, использует для самообразования различные источники информации | |||
Date: 2015-10-18; view: 487; Нарушение авторских прав