Задания для текущего контроля и способов быстрой проверки и оценки его результатов

Вариант №1	Вариант №2
1. Сформулируйте следующие определения
Что такое вектор? Что такое длина вектора? Какие векторы называются коллинеарным?	Какой вектор называется нулевым? Какие векторы называются равными? Какие векторы называются сонаправленными?
2. Даны векторы: .
Укажите пары коллинеарных векторов.	Укажите пары противоположно направленных векторов.
3. Вычислите скалярное произведение векторов и , если

Билет № 22. Прямая на плоскости.

Пусть на плоскости задана некоторая аффинная система координат и прямая l.

I. Каноническое уравнение прямой. Выберем произвольную точку M₀(x₀; y₀ ) Î l и зафиксируем направляющий вектор a (a, b) этой прямой. Тогда справедливы следующие эквивалентности: X(x; y) Î l Û (x–x₀; y–y₀) || a (a; b)Û = Û Û = 0. Итак, координаты точек, расположенных на прямой l, и только они удовлетворяют следующим эквивалентным друг другу каноническим уравнениям прямой:

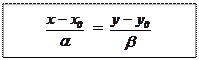
II. Параметрическое уравнение прямой. Из теории определителей известно, что Û $ t Î R Û $ t Î R 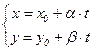. Таким образом, получаем параметрическое уравнение прямой:

III. Общее уравнение прямой. Преобразуем каноническое уравнение прямой: Û b×(x–x₀)–a×(y–y₀ ) = 0 Û b×x+(–a)×y+(–b×x₀+a×y₀) = 0 Û A×x+B×y+C = 0, где A = b, B = –a, C = –b×x₀+a×y₀ и A²+B² ¹ 0, т.к. координаты a, b направляющего вектора одновременно не обращаются в ноль.

Пусть теперь задано уравнение A×x+B×y+C = 0, где A²+B² ¹ 0. Докажем, что множество L = {M(x; y) Î p | A×x+B×y+C = 0 } является прямой на плоскости. Действительно, выберем в множестве L произвольную точку M₀(x₀; y₀ ): это всегда можно сделать, т.к. коэффициенты A, B не равны одновременно нулю (например, если B ¹ 0, то x₀ можно выбрать произвольно, а y₀ = – ×x₀– ). Таким образом, A×x₀+B×y₀+C = 0, т.е. С = –A×x₀–B×y₀. Если теперь положить a = –B, b = A и рассмотреть вектор а (a; b), то а ¹ 0 т.к. a²+b² = = A²+B² ¹ 0 и можно через т. M₀(x₀; y₀) провести прямую l с направляющим вектором а. Ввиду предыдущих эквивалентностей (с учётом A = b, B = –a, C = –b×x₀+a×y₀ и A²+B² ¹ 0) получаем A×x+B×y+C = 0 Û – каноническое уравнение прямой l.

Итак, любая прямая l может быть задана с помощью уравнения A×x+B×y+C = 0 (A²+B² ¹ 0), которое называется общим уравнением прямой на плоскости. Обратно, каждое общее уравнение A×x+B×y+C = 0 (A²+B² ¹ 0) задаёт на плоскости некоторую прямую с направляющим вектором а (–B; A).

Теорема (об общем уравнении прямой на плоскости). (1) Каждая прямая на плоскости задаётся некоторым общим уравнением вида A×x+B×y+C = 0 (A²+B² ¹ 0).

(2) Каждое общее уравнение A×x+B×y+C = 0 (A²+B² ¹ 0) однозначно определяет некоторую прямую на плоскости.

(3) Два общих уравнения A₁×x+B₁×y+C₁ = 0, A₂×x+B₂×y+C₂ = 0 (A₁²+B₁² ¹ 0 ¹ A₂²+B₂²), задают одну и ту же прямую на плоскости тогда и только тогда, когда коэффициенты этих уравнений пропорциональны: = = = l Î R \ {0}.

(4) При аффинной замене координат общее уравнение прямой преобразуется снова в общее уравнение прямой, т.е. вид общего уравнения прямой инвариантен при аффинных преобразованиях координат.

IV. Уравнение прямой в отрезках. Полученное уравнение + = 1 называется уравнением прямой в отрезках. Смысл названия раскроется, если выяснить геометрический смысл величин a, b: эта прямая пересекает ось x в точке (a; 0), а ось y – в точке (0; b). Таким образом, величины a и b определяют отрезки, отсекаемые прямой на координатных осях (см. рис).

V. Нормальное уравнение прямой. Любую прямую можно задать уравнением A×x+B×y+C = 0, где A²+B² = 1, которое называют нормальным уравнением прямой. Смысл этого названия можно понять, если ввести следующее определение: вектор единичной длины, перепендикулярный к заданной прямой, называется вектором нормали для этой прямой.

VI. Уравнение прямой с угловым коэффициентом. Пусть, по-прежнему, система координат декартова, и на плоскости дана прямая A×x+B×y+C = 0, (A²+B² ¹ 0), не параллельная оси ординат, т.е. a (–B; A) e₂ (0; 1) Û ¹ или B ¹ 0. Тогда A×x+B×y+C = 0 Û Û y = k×x+b, где k = , b = . Уравнение вида y = k×x+b называется уравнением прямой с угловым коэффициентом k.

Выясним геометрический смысл углового коэффициента k. Ясно, что прямая, параллельная оси абсцисс, имеет уравнение y = b и угловой коэффициент k = 0.

В случае k ¹ 0 можно в­зять любые две различные точки на прямой: M₀(x₀ ; k×x₀+b) и M₁(x₁; k×x₁+b). Тогда вектор a = (x₁–x₀; k×(x₁–x₀)) будет направляющим и k = = –tg a = –tg(p–j) = tg j (см. рис.). Здесь рассмотрен случай k < 0.

Т.о., угловой коэффициент k – это тангенс угла наклона прямой, т.е. угла между прямой и осью абсцисс, отсчитываемого от оси абсцисс до прямой против часовой стрелки. В случае, когда прямая параллельна оси абсцисс или совпадает с ней, угол её наклона считается равным нулю.

Пример. Написать все виды уравнений прямой, делящей стороны AB и AC треугольника ABC в отношении соответственно, если A(–5; 6), B(3; –4), C(8; 8) (система координат декартова).

Решение. Прямая проходит через точки D(a; b) и E(g; d) со свойствами (a+5; b–6)= = × 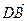(3–a; –4–b) и (g+5; d–6) = × (8–g; 8–d). Поэтому 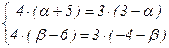и , т.е. D(– ; ) и E(; ), (; ).

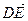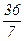Итак, пишем уравнения прямой, проходящей через точку D(– ; ) с направляющим вектором а (5; 12) || .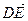

1) каноническое уравнение прямой (DE): = или = 0.

2) параметрическое уравнение прямой (DE): , (t Î R ).

3) общее уравнение прямой (DE): 12×(7×x+11) = 5×(7×y–12) или после преобразований 84×x–35×y+192 = 0.

4) уравнение прямой (DE) в отрезках: + = 1.

5) нормальное уравнение прямой (DE): ×x – ×y+ = 0.

6) уравнение прямой (DE) с угловым коэффициентом: y = ×x + .

Date: 2015-10-18; view: 406; Нарушение авторских прав