
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Поняття вектора та лінійні операції над векторами
|
|
У математиці та прикладних дисциплінах розглядаються як скалярні, так і векторні величини.
Скалярна величина характеризується тільки своїм числовим значенням, наприклад: маса, енергія, площа, об’єм та інше.
Вектором називається величина, що характеризується як числовим значенням, так і напрямком, наприклад: швидкість, прискорення, сила. Вектор, як направлений відрізок, позначається 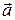 або
або  (точка
(точка  – початок і точка
– початок і точка  – кінець вектора).
– кінець вектора).
Вектор має довжину та напрямок. Довжина вектора називається модулем та позначається  або
або  .
.
Одиничним вектором або ортом називається вектор, довжина якого дорівнює одиниці. Нульовим вектором називається вектор, якщо його довжина дорівнює нулеві.
Два вектори називаються протилежними, якщо вони мають однаковий модуль та протилежний напрямок.
Два вектори називаються колінеарними, якщо вони розташовані на одній або паралельних прямих.
Три вектори називаються компланарними, якщо вони розміщені в одній площині, або паралельні одній і тій же площині.
Лінійні операції над векторами:
1) Додавання векторів.
Два вектори геометрично додаються за правилом паралелограма або правилом трикутника.
Правило паралелограма: вектор  є сумою двох векторів
є сумою двох векторів 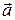 та
та  , тобто
, тобто  , якщо вектор
, якщо вектор  розташований на діагоналі паралелограма, який побудований на векторах
розташований на діагоналі паралелограма, який побудований на векторах 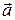 та
та  , як на його сторонах, причому початок вектора
, як на його сторонах, причому початок вектора  співпадає з початком векторів
співпадає з початком векторів 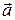 та
та  (рис. 2.1).
(рис. 2.1).

| 
|
| Рис. 2.1 | Рис. 2.2 |
Правило трикутника: вектор  є сумою двох векторів
є сумою двох векторів 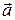 та
та  , тобто
, тобто  , якщо початок вектора
, якщо початок вектора  співпадає з початком вектора
співпадає з початком вектора 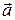 , кінець вектора
, кінець вектора  - з кінцем вектора
- з кінцем вектора  , причому початок вектора
, причому початок вектора  повинен співпадати з кінцем вектора
повинен співпадати з кінцем вектора 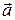 (рис. 2.2).
(рис. 2.2).
Властивості суми векторів:
-  ;
;
-  ;
;
-  ;
;
-  .
.
2) Віднімання векторів.
Різницею двох векторів 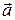 та
та  є третій вектор
є третій вектор  , який в сумі з вектором
, який в сумі з вектором  дорівнюють вектору
дорівнюють вектору 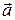 (рис. 2.3).
(рис. 2.3).
3) Множення вектора на скаляр.
Добутком вектора 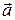 на скаляр
на скаляр  є вектор
є вектор  , довжина якого дорівнює
, довжина якого дорівнює  , якщо
, якщо  вектор
вектор  має той же напрямок, що і вектор
має той же напрямок, що і вектор 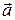 ; якщо
; якщо  вектор
вектор  направлений у протилежну сторону вектора
направлений у протилежну сторону вектора 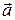 (приклади на рис.º2.4).
(приклади на рис.º2.4).

| 
|
| Рис. 2.3 | Рис. 2.4 |
Властивості множення вектора на скаляр:
-  ;
;
-  ;
;
-  .
.
Нехай маємо  векторів
векторів 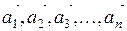 та
та  скалярних величин
скалярних величин  .
.
Запишемо лінійну комбінацію цих векторів, використовуючи скаляри, тобто розглянемо суму векторів  .
.
Складемо рівність:
 . .
| (2.1) |
Якщо виконується рівність (2.1) при умові  , то вектори
, то вектори 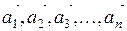 називаються лінійно незалежними.
називаються лінійно незалежними.
Якщо рівність (2.1) виконується і хоча б частина скалярів  не дорівнює нулеві, то ці вектори називаються лінійно залежними.
не дорівнює нулеві, то ці вектори називаються лінійно залежними.
Іншими словами, вектори називаються лінійно залежними, якщо будь-який з них можна виразити через лінійну комбінацію інших.
Проекція вектор на вісь
Нехай існує вектор 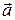 та вісь
та вісь  (рис. 2.5). Вектор
(рис. 2.5). Вектор  ,
,  – кут між вектором
– кут між вектором 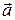 та віссю
та віссю  , точки
, точки  та
та  – проекції точок
– проекції точок  та
та  на вісь.
на вісь.
Проекцією  вектора
вектора 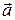 та вісь
та вісь  буде величина відрізка
буде величина відрізка  .
.

|
| Рис. 2.5 |
Проекція  вектора
вектора 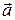 та вісь
та вісь  дорівнює добутку довжини вектора
дорівнює добутку довжини вектора  на косинус кута між напрямком вектора
на косинус кута між напрямком вектора 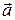 та додатнім напрямком осі
та додатнім напрямком осі  :
:
 . .
| (2.2) |
Оскільки  може бути в залежності від значення кута
може бути в залежності від значення кута  додатною або від’ємною величиною, то і проекція вектора на вісь може мати: знак „+”, якщо кут
додатною або від’ємною величиною, то і проекція вектора на вісь може мати: знак „+”, якщо кут  –гострий; знак „–”, якщо кут
–гострий; знак „–”, якщо кут  –тупий.
–тупий.
Властивості проекції на вісь:
- 
-  ;
;
-  ;
;
- проекція замкнутої векторної лінії на вісь дорівнює нулю.
Date: 2015-10-18; view: 445; Нарушение авторских прав