Матриці та дії над ними

Вступ

Методичні вказівки та індивідуальні завдання з курсу вищої математики за темами „Лінійна та векторна алгебра” та „Аналітична геометрія на площині та у просторі” складено відповідно до програми курсу.

Мета розробки: перевірка знань студентів з основних понять і методів курсу, прищеплення у студентів навичок самостійної роботи.

Типові розрахунки можуть бути використані викладачами для контролю знань студентів, для проведення аудиторних індивідуальних практичних занять, а також як домашні індивідуальні завдання.

Розділ 1. Лінійна алгебра

Матриці та дії над ними

Поняття матриці та відповідний розділ математики мають важливе значення для економістів, оскільки велика кількість досліджувальних об’єктів і процесів досить просто, а головне – компактно, подається в матричній формі.

Матрицею розміру називається множина з 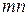елементів , розміщених у вигляді прямокутної таблиці з рядків і стовпців:

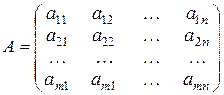
	(1.1)
,	(1.2)

де – елемент матриці; – номер рядка; – номер стовпця.

Матриці бувають різних типів: прямокутні, квадратні, діагональні, одиничні, нульові та інші.

Квадратною матрицею називається матриця, в якій кількість рядків і стовпців однакова. Їх кількість вказує розмір матриці. Головною діагоналлю квадратної матриці називається діагональ, яка проходить через верхній лівий та нижній правий кути матриці, тобто сукупність елементів .

Квадратну матрицю, в якій всі елементи, окрім тих, що розташовані на головній діагоналі, дорівнюють нулю, називають діагональною матрицею.

Діагональну матрицю, в якій всі елементи дорівнюють одиниці, називають одиничною і позначають літерою .

.

(1.3)

Матриця називається трикутною, якщо всі її елементи під (над) діагоналлю дорівнюють нулю.

Нульовою матрицею називається матриця, всі елементи якої дорівнюють нулю.

Над матрицями, як і над числами, можна виконувати різні операції, причому деякі з них – аналогічні операціям над числами, а деякі – специфічні.

Розрізняють наступні дії над матрицями:

1. Операція порівняння: дві матриці та називаються рівними , якщо рівні їх відповідні елементи, тобто .

2. Множення матриці на число: добутком матриці на число називається матриця , елементи якої визначаються за формулою

.

(1.4)

3. Додавання та віднімання матриць: сумою двох матриць і називається матриця , елементи якої визначаються за формулою

.

(1.5)

Додавати можна матриці лише однакового розміру, тобто матриці з однаковою кількістю рядків і стовпців.

Властивості операцій додавання та віднімання матриць:

- (комутативність);

- (асоціативність);

- (дистрибутивність);

- (нейтральність нульової матриці).

4. Транспонування матриці: транспонованою матрицею до матриці називається така матриця, в якій рядки та стовпці міняються місцями, і позначається літерою .

5. Множення матриць: добутком двох матриць і називається матриця , елементи якої визначаються за формулою

.

(1.6)

Перемножать можливо лише такі дві матриці, в яких кількість стовпців першої збігається з кількістю рядків другої:

.

(1.7)

Добутком двох матриць є матриця, в якій кількість рядків дорівнює кількості рядків першої матриці, а кількість стовпців – кількості стовпців другої матриці.

Властивості добутку матриць:

- ;

- ;

- ;

- ;

- ;

- .

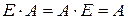Date: 2015-10-18; view: 635; Нарушение авторских прав