Означення та основні властивості визначників

Квадратній матриці можна поставити у відповідність число, що обчислюється за певним правилом і називається визначником. Його позначають символом або . Правило, за яким обчислюється визначник, залежить від порядку матриці.

Визначник другого порядку обчислюється наступним чином:

.

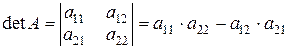(1.8)

Визначник другого порядку дорівнює різниці добутків елементів головної та побічної діагоналі.

Визначником третього порядку називається число, що обчислюється за таким правилом:

.

(1.9)

Формула (1.9) – це формула „трикутника” для обчислення визначника третього порядку. Якщо елементи матриці третього порядку позначити точками, то три доданки, що беруться зі знаком „+”, лежать на головній діагоналі й у вершинах трикутників, одна із сторін яких паралельна головній діагоналі (рис.1.1).

Рис.1.1

Аналогічні співмножники від’ємних доданків лежать на побічній діагоналі й у вершинах трикутників, одна із сторін яких паралельна їй (рис.1.2).

Рис.1.2

За іншою схемою дописують два перші стовпці до матриці, внаслідок чого одержують прямокутну матрицю розміром . Тоді додатні та від’ємні доданки формули (1.9) беруть за схемою (правило Саррюса), зображеною на рис.1.3.

Рис.1.3

Мінором елемента визначника називається визначник меншого на одиницю порядку, отриманий із даного шляхом викреслення з нього -го рядка та -го стовпця.

Алгебраїчним доповненням елемента визначника називається величина, яку знаходять за формулою

.

(1.10)

Визначник дорівнює сумі добутків будь-якого рядка чи стовпця на їхні алгебраїчні доповнення.

Властивості визначників:

- значення визначника не зміниться при його транспонуванні (тобто замінити рядки стовпцями і навпаки);

- якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то і сам визначник дорівнює нулю;

- якщо у визначнику поміняти місцями два сусідні рядки чи стовпці, то знаки таких визначників будуть протилежними, а їх абсолютні значення – однаковими;

- визначник із двома однаковими рядками чи стовпцями дорівнює нулю;

- якщо деякий рядок чи стовпець визначника помножити на довільне число , то значення визначника зміниться у разів;

- значення визначника не зміниться, якщо до будь-якого рядка додати інший, помножений на довільне число або лінійну комбінацію інших рядків;

- сума добутків усіх елементів деякого рядка або стовпця на алгебраїчні доповнення до іншого рядка або стовпця визначника дорівнює нулю;

- якщо елементи будь-якого ряду визначника можна подати у вигляді суми, то цей визначник можна подати у вигляді деяких визначників;

- сума добутків елементів будь-якого ряду визначника на алгебраїчні доповнення, які відповідають елементам іншого паралельного ряду, дорівнює нулю.

У матричному численні важливу роль відіграває поняття оберненої матриці.

Матриця , яка задовольняє співвідношення

(1.11)

називається оберненою до матриці і позначається .

Для того, щоб квадратна матриця мала обернену матрицю, необхідно і достатньо, щоб її визначник не дорівнював нулю. Обернену матрицю можна знайти різними способами. Один із них полягає у побудові приєднаної матриці. Транспонована матриця, яка складена із алгебраїчних доповнень до їх елементів, називається приєднаною і позначається :

.

(1.12)

Тоді обернену матрицю можливо знайти наступним чином:

.

(1.13)

Date: 2015-10-18; view: 515; Нарушение авторских прав