
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Потеря напряжения в проводах
|
|
Как видно из предыдущих рассуждений, напряжение Uи в начале линии (на зажимах источника) меньше ЭДС на величину падения напряжения в источнике энергии (Uи=Еи - Irви), а напряжение Uп на зажимах приёмника меньше Uи на величину падения напряжения в линии.
Уменьшение напряжения при передаче электроэнергии по проводам называется изменением или потерей напряжения в линии и для цепей постоянного тока равно падению напряжения на соответствующем участком цепи.
Практически обычно рассчитывают отклонение напряжение от номинального значения при колебаниях нагрузки. Отклонение напряжения в сторону уменьшения ограничено тем, что при снижении напряжения значительно ухудшаются выходные характеристики потребителей электрической энергии, резко уменьшается световой поток лампы накаливания, электрические двигатели требуют токи, превосходящие номинальные.
При отклонении напряжении в сторону увеличения лампы накаливания, например, могут быстро выйти из строя, а электродвигатели будут работать в недопустимых условиях.
Поэтому отклонения напряжения в промышленных сетях имеют жёсткие допуски:
- в сторону уменьшения 2,5 … 5%;
- в сторону увеличения 5%;
В бортовых сетях:
- постоянный ток (+ 5 … - 10%) = 28 В;
- переменный ток (+ 2 … - 3%) ~ 200 В;
В трёхфазных генераторах последнего поколения ± 0,5%.
Расчёт линии по отклонениям напряжения для наибольшей и наименьшей нагрузок следующий:
- определение сечения проводов (может быть поставлена обратная задача: определение потерь и отклонения напряжения для линии при данных сечениях проводов и нагрузок);
- выбор или проверка сечения проводов линии без их перегревания при протекании тока (здесь также может быть поставлена обратная задача: проверка имеющихся проводов определенного сечения на отсутствие перегрева).
| Uu |
| Uп |
| Rл |
| + |
| - |
| I |
| Eн |
| rn |
| I |
| L |
Рис. 1.11
Напряжение в начале двухпроводной линии Uи (рис. 1.11), соединяющей источник энергии с каким-либо приёмником (например, электродвигателем, группой ламп и т.д., обозначаемых условно нагрузкой rп), определится из формулы: Uп=UИ- 2I Rл ,
отсюда Uи=Uп+2I Rл (1.20),
где Uп – напряжение на конце линии (на зажимах приемника);
Rл – сопротивление каждого провода линии.
Разность напряжений в начале и конце линии Uи и Uп называется потерей напряжения в линии и обозначается ∆Uл:
∆Uл = Uи - Uп = 2I Rл (1.21)
Из физики известно, что Rл =  (1.22),
(1.22),
следовательно, ∆Uл = I  (1.23),
(1.23),
где L – длина одного провода в линии, м;
S – площадь поперечного сечения проводов, мм2;
 – удельное сопротивление материалов проводов, Ом*мм2/м; (в системе СИ единицей удельного сопротивления
– удельное сопротивление материалов проводов, Ом*мм2/м; (в системе СИ единицей удельного сопротивления  является Ом*м, 10мм=106 Ом*мм2/м).
является Ом*м, 10мм=106 Ом*мм2/м).
Относительная потеря напряжения в линии, т.е. потеря напряжения в процентах определяется как
 (1.24)
(1.24)
Зная ток I и наибольшую допустимую потерю напряжения ∆UЛдоп, можно найти необходимое сечение проводов ∆UЛдоп =  , отсюда
, отсюда
S =  (1.25)
(1.25)
Подсчитанное по этой формуле сечение проводника округляется до ближайшего стандартного (в сторону увеличения).
Потери мощности в линии:
∆Pл = ∆Uл I = 2I2 RЛ (1.26)
С потерей напряжения и мощности в линии тесно связан коэффициент полезного действия линии ηл, определяемый как отношение отдаваемой линией приёмнику мощности Рп к получаемой ею от источника энергии мощности Ри:
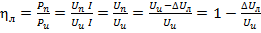 (1.27)
(1.27)
или в процентах:
 (1.28)
(1.28)
Чем меньше потери напряжения в линии, тем больше КПД линии.
Вместо КПД линии часто рассматривается величина (коэффициент) относительной потери мощности в ней.
 ;
;  (1.29),
(1.29),
то есть относительная потеря мощности в двухпроводной линии постоянного тока равна относительной потере напряжения в ней.
Из выражения для ө получаем при умножении числителя и знаменателя на Uи
 (1.30)
(1.30)
Отсюда видно, что при передаче данной мощности потери напряжения в проводах обратно пропорциональны квадрату напряжения источника энергии.
Как видно из последнего выражения (1.30), с увеличением длины провода для передачи требуемой мощности при заданных потерях и приемлемом сечении проводов необходимо повышать напряжения Uи источника энергии. При этом относительная величина потери напряжения уменьшатся обратно пропорционально квадрату напряжения. Поэтому передача больших мощностей на дальние расстояния осуществляется по линиям высокого напряжения.
1.1.4. Расчёт электрической цепи при помощи уравнений Кирхгофа
Существует ряд методов расчёта токов в разветвлённой цепи. Все эти методы исследования цепей основаны на применении закона Ома и двух законов Г.Р. Кирхгофа, немецкого физика, основоположника спектрального анализа (1824-1887).
Первый закон Кирхгофа выражает факт непрерывности тока: ни в одной точке цепи не происходит накопление электрических зарядов.
Таким образом, в узле электрической цепи А, где сходятся n проводов (рис. 1.12), не может быть накопления зарядов, поэтому сумма зарядов, текущих в любой момент времени к узлу А, равна сумме зарядов, уходящих от узла.
| A |
| I4 |
| I3 |
| I2 |
| I1 |
| In |
| In-1 |
Рис. 1.12
Алгебраическая сумма токов в проводах, сходящихся в любом узле электрической цепи, равна нулю, т.е. математически это можно выразить следующей записью:

где n – общее количество проводов, сходящихся в узле электрической цепи;
k – порядковый номер провода.
При этом токи, текущие к узлу цепи, следует брать с одним знаком (обычно считают их положительными), а токи, текущие от узла, - с другим знаком (отрицательными).
Второй закон Кирхгофа устанавливает связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре, который можно выделить в рассматриваемой электрической цепи. Этот закон в математической форме выражает то, вытекающее из закона сохранения энергии положение, что изменение потенциала при обходе замкнутого контура равно нулю, то есть устанавливается математическая связь между ЭДС, действующей в замкнутой электрической цепи, и произведениями токов в ветвях цепи на сопротивление ветвей.
| A |
| B |
| C |
| D |
| r1 |
| r2 |
| r3 |
| r4 |
| I1 |
| I2 |
| I3 |
| I4 |
| E1,rв1 |
| E2,rв2 |
| E4,rв4 |
Рис. 1.13
В рассматриваемой на рис. 1.13 замкнутой электрической цепи ABCD действует три ЭДС: Е1, Е2 и Е4, причём две из них Е1 и Е2 действуют согласно в одном направлении (по ходу контура), а третья Е4– навстречу. Следовательно, выбрав направление обхода контура ABCD по часовой стрелке (показано внутри контура) и считая ЭДС, действующие в направлении обхода, положительными, а ЭДС, действующие в обратном направлении - отрицательными, определим результирующую ЭДС:
Е=Е1+Е2-Е4 (1.32)
Результирующая ЭДС Е будет затрачиваться на проведение тока в ветвях цепи и в соответствии с законом Ома будет равно сумме произведений токов на сопротивления ветвей:
Е = I1 (r1 + rв1) + I2(r2 + rв2) - I3r3 - I4 (r4 + rв4) (1.33)
В правой части равенства произведения токов I3 и I4 на соответствующие сопротивления взяты со знаком минус, т.к. эти токи протекают против принятого направления обхода контура.
Для цепи, имеющей n ветвей, получим равенство:

математически выражающее второй закон Кирхгофа: алгебраическая сумма ЭДС, действующих в любом замкнутом контуре, равна алгебраической сумме падений напряжений в ветвях этого контура.
| I |
| r1 |
| r2 |
| r4 |
| r3 |
| U1 |
| U2 |
| U3 |
| U4 |
| Uu = Eu - Irв |
| Eu ,rв |
Рис. 1.14
Для электрической цепи с последовательным соединением резисторов (рис. 1.14) по второму закону Кирхгофа можно записать выражение:
Uu= U1 + U2 + U3+U4 = Ir1 + Ir2 + Ir3 + Ir4 = I (r1 + r2 + r3 + r4)=I Rэпосл (1.35)
или Еи = I (Rэпосл + rв) (1.36)
Отсюда следует, что при последовательном соединении резисторов общее сопротивление цепи равно сумме сопротивлений этих резисторов:

| I1 |
| U1 |
| r1 |
| Uu |
| I2 |
| U2 |
| r2 |
| I3 |
| U3 |
| r3 |
| I4 |
| U4 |
| r4 |
| I |
| I |
| Eu,rв |
Рис. 1.15
Для электрической цепи с параллельным соединением резисторов (рис. 1.15) напряжения на их зажимах одинаково:
Uи = U1 = U2 = U3 = U4 = I r1 = I r2 = I r3 = I r4 = U (1.38)
В соответствии с первым законом Кирхгофа ток цепи I равен сумме токов параллельных ветвей:
I = I1 + I2 + I3 + I4 (1.39)
Применяя закон Ома для каждой ветви (участка цепи) получим:
 (1.40),
(1.40),
где qэпарал – общая (эквивалентная) проводимость цепи при параллельном соединении резисторов.
Отсюда следует, что при параллельном соединении резисторов общая проводимость цепи равна сумме проводимостей параллельных ветвей:


Из выражения для токов в каждой параллельной ветви получим:
I1=U 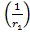 =Uq1=I
=Uq1=I  q1=I
q1=I 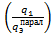 ;
;
I2=U 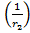 =Uq2=I
=Uq2=I  q2=I
q2=I  ;
;
I3=U 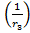 =Uq3=I
=Uq3=I  q3=I
q3=I  ;
;
……………………………………..;
In=U  =Uqn=I
=Uqn=I  qn=I
qn=I 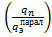 . (1.43).
. (1.43).
Отсюда можно заметить, что если дан общий ток I, то отдельные токи в ветвях I1, I2, I3, …, In распределяются пропорционально проводимостям резисторов.
Мощность цепи с параллельным соединением резисторов складывается из мощностей отдельных ветвей:

Смешанное соединение резисторов в цепи постоянного тока представлено на рис. 1.16.
| I2 |
| I |
| I1=I |
| I3 |
| I |
| r1 |
| r2 |
| r3 |
| а |
| б |
| E, r1 |
Рис. 1.16
Вначале вычислим сопротивление участка а – б с параллельным соединением
резисторов
 (1.45)
(1.45)
Общее сопротивление цепи определится как эквивалентное сопротивление при последовательном соединении резисторов:
 (1.46)
(1.46)
Из данного примера для смешанного соединения резисторов в простой электрической цепи следует метод определения эквивалентного сопротивления в общем случае при сколь угодно большом числе участков цепи.
Суть его заключается в строгой последовательности проведения расчётов цепи: сначала находятся эквивалентные сопротивления участков, затем эквивалентное сопротивление всей цепи определяется как сумма найденных эквивалентных сопротивлений и сопротивлений других одиночных резисторов, включённых последовательно.
Источники энергии называются включёнными параллельно, если у них ЭДС направлены к одному и тому же узлу (рис. 1.17). Иначе говоря, все положительные зажимы источников должны быть присоединены к одному узлу, а все отрицательные – к другому (на борту воздушного судна “плюс” на шине и “минус” на корпусе соответственно).
| E1 rв1 |
| E2 rв2 |
| + |
| - |
| + |
| - |
| I1 |
| I2 |
| I |
| r |
| а |
| б |
| U |
Рис. 1.17
Распределение тока нагрузки I между параллельно соединёнными источниками зависит от их ЭДС и внутренних сопротивлений.
Напряжение U на зажимах а- б связано с ЭДС и внутренними сопротивлениями источников следующим соотношениями:
U = E1 - I1 rв1
U = E2 - I2 rв2
Отсюда
E1 - I1 rв1 = E2 - I2 rв2.
или
E1 - E2 = I1 rв1- I2 rв2 (1.47)
Причём по первому закону Кирхгофа
I = I1 - I2 или I2 = I - I1 (1.48)
Подставляя выражение для I2 в предыдущее уравнение (1.47), получим:
Е1 - Е2 = I1 rв1 - (I - I1 ) rв2 = I1 rв1 – I rв2 - I1 rв2 = I1 (rв1 - rв2) - Irв2 (1.49)
Отсюда:
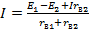 (1.50)
(1.50)
или
 (1.51)
(1.51)
Аналогично для тока I2 получим:
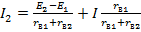 (1.52)
(1.52)
Первый член правых частей выражений для I2 и I1 представляет собой ток соответствующего источника при отсутствии нагрузки (если I=0, то r→∞, что может быть при разрыве цепи нагрузки), при этом если Е1=Е2, токи источников равны нулю, т.е. I1=I2=0.
Второй член правой части этих выражений определяет по существу распределение тока I между двумя параллельно включёнными сопротивлениями rв1 и rв2, при этом если Е1=Е2=0 (при условии 0 ≤ r < ∞), ток нагрузки распределяется между источниками энергии обратно пропорционально их внутренним сопротивлениям, а если Е1 ≠ Е2, то в цепи источников появляется ещё уравнительный ток, выражаемый первым членом правой части рассматриваемых формул:
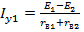 ;
; 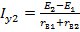 (1.53)
(1.53)
Направление уравнительных токов зависит от знака числителя в формулах, определяющих их количественное значение, т.е. численного соотношения Е1 и Е2.
Рассмотрим применение законов Кирхгофа для расчёта сложных электрических цепей. Общей задачей расчёта является определение токов во всех участках сложной цепи (т.е. цепи, имеющей сложную конфигурацию) при заданных параметрах элементов цепи в известной её конфигурации.
Рассматриваемый метод заключается в составлении уравнений по первому и второму закону Кирхгофа для узлов и контуров электрической цепи. При решении этих уравнений находятся неизвестные токи ветвей.
Общее правило составления уравнения:
- общее число уравнений исходя из правил их решения должно быть равно числу неизвестных токов (определяемых значений токов в ветвях цепи), т.е. числу ветвей цепи;
- число уравнений, которые можно составить на основании первого закона Кирхгофа, равно числу узлов цепи, уменьшенному на единицу;
- недостающие уравнения составляются по второму закону Кирхгофа.
При этом следует начинать с наиболее простого контура и следить за тем, чтобы каждый следующий контур, для которого пишется уравнение, содержал хотя бы одну ветвь, не вошедшую в уже обойдённые контуры.
Практически число уравнений, которые можно составить по первому и второму законам Кирхгофа, всегда больше числа неизвестных токов, равного числу ветвей цепи. Поэтому желательно заранее составить рациональную систему уравнений, то есть установить, сколько уравнений следует написать по первому и сколько по второму законам Кирхгофа для получения системы уравнений, имеющей определённые решения.
Исследуем сложную цепь, изображённую на рис 1.18.
| I2 |
| I1 |
| I3 |
| A |
| B |
| r2 |
| r1 |
| r3 |
| E1,rв1 |
| E2,rв2 |
| E3,rв3 |
Рис. 1.18
Будем считать неизвестными значения ЭДС Е1, Е2, Е3, внутренние сопротивления источников энергии rв1, rв2, rв3, а также сопротивления ветвей r1, r2, r3. Следует определить токи в трёх ветвях цепи I1, I2, I3.
Предварительно зададимся направлением токов в ветвях (на рис. 1.18 токи I1 и I2 направлены вверх к узлу А, а ток I3 – к узлу В). Если выбранные (предположительно) направления токов окажутся противоположными действительным (реальным), то при решении уравнений получим значение этих токов со знаком минус. Это будет свидетельствовать о том, что соответствующие токи текут в обратных направлениях.
Так как цепь имеет два узла (А и В), то по первому закону Кирхгофа можно составить только одно уравнение (число уравнений по первому закону Кирхгофа должно быть на единицу меньше числа узлов в цепи). Это правило вытекает из следующих тривиальных рассуждений: каждая ветвь цепи всегда соединяет два узла, и её ток является для одного из этих узлов положительным (направленным к узлу, например, токи I1 и I2 к узлу А), для другого отрицательным (те же токи, направленные от узла В).
Поэтому если написать по первому закону Кирхгофа уравнения для всех узлов цепи (в нашем случае для узлов А и В), то каждый ток войдёт в эти уравнения дважды: один раз как положительный, а другой как отрицательный, а сумма левых частей полученных уравнений будет тождественно равно нулю. Отсюда выходит, что уравнения для узлов А и В совершенно одинаковы:
I1 + I2 - I3 = 0 – для узла А (1.54)
или
- I1 - I2 + I3 = 0 – для узла В (1.55).
Первую запись уравнения (для узла А) берём за основу и включаем в составляемую систему (хотя в принципе безразлично, какая запись уравнения войдёт в систему).
Для определения трёх неизвестных токов надо составить ещё два уравнения по второму закону Кирхгофа. Эти оставшиеся два уравнения можно составить для любых двух контуров из имеющихся трёх для данной конфигурации цепи. Целесообразно написать два уравнения для контуров 1 и 2.
Казалось бы, что третье уравнение можно составить и для контура 3, хотя оно и лишнее, так как для определения трёх неизвестных уже есть достаточное количество уравнений. Но это третье уравнение, составленное по второму закону Кирхгофа явилось бы следствием первых двух, то есть для данной цепи можно составить только два линейно-независимых уравнения, так как в третьем контуре уже нет ветвей, встречающихся впервые при составлении уравнения по второму закону Кирхгофа.
Выбрав положительное направление обхода этих контуров (по часовой стрелке), составим уравнения:
I1 (r1 + rв1) - I2 (r2 + rв2) = E1 - E2 (1.56)
I2 (r2 + rв2) + I3 (r3 + rв3) = E2 - E3 (1.57)
Совместное решение уравнений, составленных по первому и второму законам Кирхгофа, даёт возможность определить токи I1, I2 и I3.
Для упрощения записи при проведении расчётов примем укороченную запись выражений, входящих в эти уравнения, например:
r1 + rв1 = R1; r2 + rв2 = R2; r3 + rв3 = R3 (1.58)
E1 - E2 = ∆Eʹ; E2 - E3 = ∆Eʹʹ (1.59)
В результате получим систему:

Решив полученную систему уравнений путём несложных математических преобразований, можно найти все три тока в ветвях цепи:
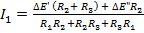 ;
;
 ; (1.60)
; (1.60)

И в развёрнутом виде через параметры элементов цепи:
 ;
;
 ; (1.61)
; (1.61)
 .
.
Метод расчёта цепи, состоящей, как показано на примере только из трёх ветвей, путём решения уравнений по законам Кирхгофа является достаточно трудоёмким. Усложнение конфигурации цепи значительно усложняет и её расчёт. Так, например, для цепи, имеющей пятнадцать ветвей, требуется составить и решить систему из 15 уравнений.
Поэтому непосредственное применение законов Кирхгофа для определения токов в сложных разветвлённых цепях требует совместного решения значительного числа уравнений, что естественно связано с большой затратой времени при ручном расчёте (т.е. без применения вычислительной техники с соответствующим программным обеспечением). Существует, однако, ряд методов, в основе которых лежат те же законы Кирхгофа, но они позволяют избежать решения системы уравнений или уменьшить число уравнений, подлежащих решению и, таким образом, значительно упростить процесс расчёта сложных электрических цепей. К таким методам относятся наиболее распространённые в практике вычислений методы контурных токов, наложения и узловых напряжений.
Date: 2015-10-21; view: 1010; Нарушение авторских прав