Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Нечіткий кластерний аналіз
Нечіткий кластерний аналіз використовується при побудові нейро-нечітких систем для визначення нечітких множин, якщо вони невідомі апріорі. Нечіткі множини знаходяться як проекції кластерів на кожну розмірність. Можливо поєднувати апріорні знання з кластерним аналізом, використовуючи його для уточнення параметрів функції приналежності. Недоліком такого методу визначення нечітких множин є складність їхньої інтерпретації.
Більшість методів нечіткої кластеризації спрямовані на мінімізацію суми:
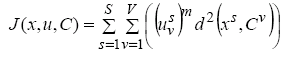при виконанні умов:
де S – кількість екземплярів, N – кількість параметрів, що описують один екземпляр (або кластер), V – кількість кластерів; x =(x 1, x 2,..., xS) T – це матриця входів для екземплярів навчаючої вибірки, xs = (xs 1, xs 2,..., xsN) – входи s -го екземпляра, s =1, 2,..., S, u = (u 1, u 2,..., uS) T – матриця приналежностей екземплярів до кожного з кластерів, us = (us 1, us 2,..., usV) – вектор приналежностей s -го екземпляра до кожного з кластерів, usv Î[0,1], C =(C 1, C 2,..., CV) T – матриця центрів кластерів, Cv = (Cv 1, Cv2, …, C vN) – центр v -го кластера, v = 1, 2,..., V, m > 1 – ступінь нечіткості отриманого розподілу (зазвичай обирається рівним 2), d (xs, Cv) – відстань між s -м екземпляром та центром v -го кластера.
Координати центрів кластерів визначають за формулою:
Найбільш простим є метод, в якому відстань між екземпляром та кластером знаходиться як евклідова відстань:
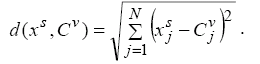Такий метод шукає кластери як сфери однакового розміру.
Більш складні методи кластеризації шукають кластери як гіпереліпсоїди різного розміру. Такі методи називають частковими, вони не можуть вірно опрацьовувати шуми та викиди і віднаходити кластери з неопуклими поверхнями. Для проведення кластерного аналізу за допомогою часткового методу необхідно задати його параметри: діапазон значень змінних, кількість кластерів для кожної із змінних (або їх ширину), функцію приналежності, що описує кластери та інші параметри в залежності від обраного методу кластеризації.
За допомогою ієрархічних методів можна віднайти кластери, об’єднуючи менші кластери та розподіляючи більші. Таким чином знаходиться дерево кластерів, на різних рівнях якого можна отримати різне розподілення на кластери.
Щільнісні методи та сіткові методи дозволяють розподіляти на кластери різного розміру довільно розподілені екземпляри. Вони також добре впізнають шуми та викиди, але потребують ретельного вибору параметрів, необхідних для реалізації методу.
Множину ознак у об’єктів кластеризації слід вибирати так, щоб всі значення ознак були виміряні в шкалі відношень або шкалі інтервалів. У цьому випадку результати нечіткої кластеризації мають змістовну інтерпретацію, адекватну проблемі знаходження нечітких кластерів.
Інтервальна шкала. В процесі виміру ознаки об’єкту ставиться у відповідність, як правило, деяке дійсне число, рівне значенню цієї ознаки. Допустимим перетворенням в шкалах інтервалів є довільна лінійна зростаюча функція між двома множинами значень ознак. Характерною властивістю цієї шкали є відсутність абсолютного нуля. Приклад ознаки, вимірюваної в інтервальній шкалі: температура в шкалах Цельсія і Фаренгейта.
Шкала відношень. В процесі виміру ознаки об'єкту ставиться у відповідність також деяке дійсне число, рівне значенню цієї ознаки. Допустимим перетворенням в шкалах відношень є довільна лінійна зростаюча функція, що проходить через нуль. Характерною властивістю цієї шкали є наявність абсолютного нуля. Приклади ознак, вимірюваних в шкалі відношень: відстань в метрах і футах, маса в кілограмах і фунтах, швидкість в км/год і вузлах.
|
Date: 2015-09-25; view: 369; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |