Виды колебаний

· Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

· Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Особую роль в колебательных процессах имеет простейший вид колебаний - гармонические колебания. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний.

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.
Уравнение гармонических колебаний имеет вид:

,
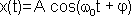где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса - называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постояннаяφ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π/ .
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота = 2π/T = 2πν дает число колебаний за 2π секунд.

Графически гармонические колебания можно изображать в виде зависимости x от t (рис.1.1.А), так и методом вращающейся амплитуды (метод векторных диаграмм) (рис.1.1.Б).

Рисунок 1.1. Графическое изображение гармонических колебаний

Метод вращающейся амплитуды позволяет наглядно представить все параметры, входящие в уравнение гармонических колебаний. Действительно, если вектор амплитуды А расположен под углом φ к оси х (см. Рисунок 1.1. Б), то его проекция на ось х будет равна: x = Acos(φ). Угол φ и есть начальная фаза. Если вектор А привести во вращение с угловой скоростью , равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:
.
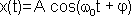Таким образом, длина вектора равна амплитуде гармонического колебания, направление вектора в начальный момент образует с осью x угол равный начальной фазе колебаний φ, а изменение угла направления от времени равно фазе гармонических колебаний. Время, за которое вектор амплитуды делает один полный оборот, равно периоду Т гармонических колебаний. Число оборотов вектора в секунду равно частоте колебаний ν.

1. Распространение колебаний в биологических средах. Поперечные и продольные волны

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

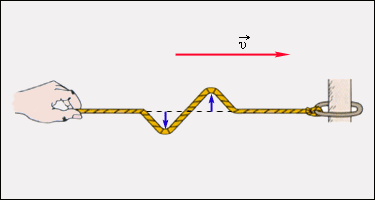
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.

Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.

Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Рисунок 2.6.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту

Рисунок 2.6.2. Распространение продольного волнового импульса по упругому стержню

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладатьинертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде от частицы к частице с некоторой скоростью v.

Например, если в жидкую или газообразную среду поместить колеблющееся тело, то колебательное движение тела будет передаваться прилегающим к нему частицам среды. Они, в свою очередь, вовлекают в колебательное движение соседние частицы и так далее. При этом все точки среды совершают колебания с одинаковой частотой, равной частоте колебания тела. Эта частота называется частотой волны.

Волной называется процесс распространения механических колебаний в упругой среде.

Частотой волны называется частота колебаний точек среды, в которой распространяется волна.

С волной связан перенос энергии колебаний от источника колебаний к периферийным участкам среды. При этом в среде возникают

периодические деформации, которые переносятся волной из одной точки среды в другую. Сами частицы среды не перемещаются вместе с волной, а колеблются около своих положений равновесия. Поэтому распространение волны не сопровождается переносом вещества.

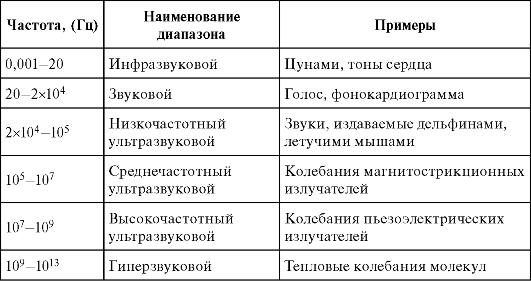
В соответствии с частотой механические волны делятся на различные диапазоны, которые указаны в табл. 2.1.

Таблица 2.1. Шкала механических волн

В зависимости от направления колебаний частиц по отношению к направлению распространения волны, различают продольные и поперечные волны.

Продольные волны - волны, при распространении которых частицы среды колеблются вдоль той же прямой, по которой распространяется волна. При этом в среде чередуются области сжатия и разряжения.

Продольные механические волны могут возникать во всех средах (твердых, жидких и газообразных).

Поперечные волны - волны, при распространении которых частицы колеблются перпендикулярно направлению распространения волны. При этом в среде возникают периодические деформации сдвига.

В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому поперечные волны в этих средах не образуются. Исключение составляют волны на поверхности жидкости.

Date: 2015-09-24; view: 1051; Нарушение авторских прав