Элементы теории

Вычисление частных производных производится по тем же правилам, что и вычисление функций одной переменной, считая все переменные постоянными, кроме той, по которой ведется дифференцирование.

Первым дифференциалом называют линейную относительно приращений 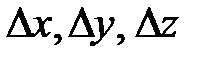часть полного приращения функции, которая для функции двух переменных имеет вид:

,

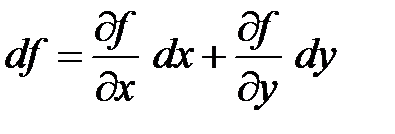а для функции трех переменных:

.

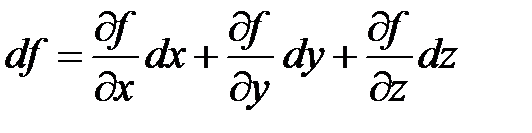Производная по направлению задает скорость изменения функции в заданной точке по заданному направлению :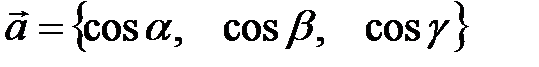

.

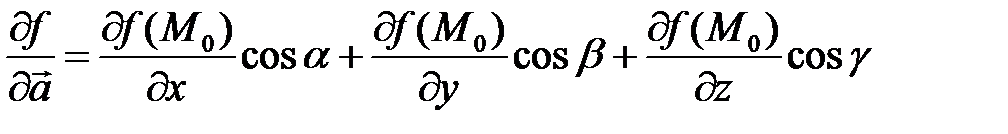Градиентом дифференцируемой функции называют вектор, координатами которого являются частные производные в заданной точке:

.

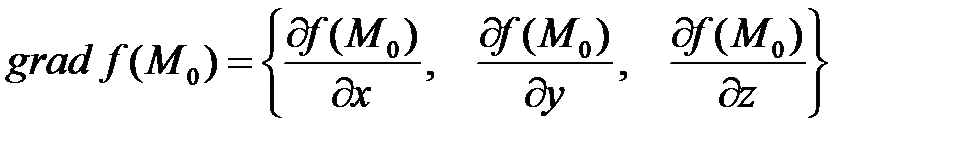Производная по направлению является проекцией вектора градиента на это направление:

.

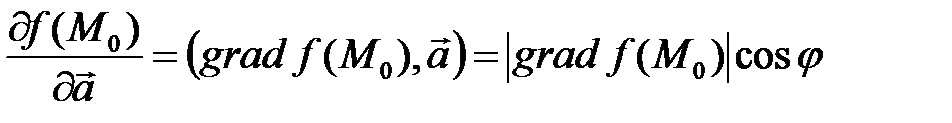Анализ последнего выражения показывает, что градиент является направлением, скорость изменения функции вдоль которого максимальна.

Касательная плоскость содержит касательные ко всем кривым, проходящим через данную точку поверхности :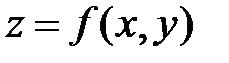

.

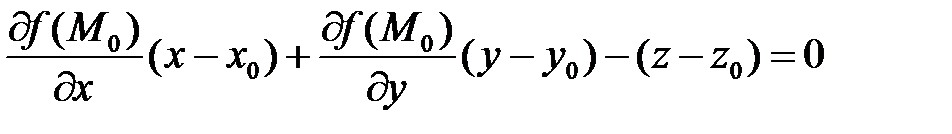Производную сложной функции 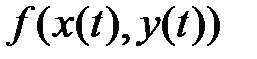находим по правилу

,

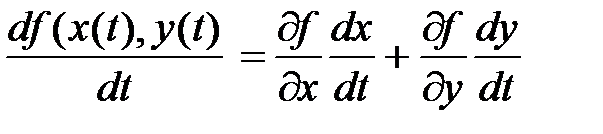а производные сложной функции 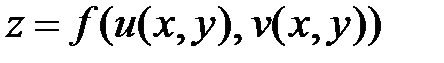согласно правилу:

.

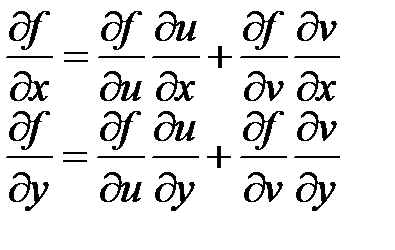Производную функции, заданной неявно 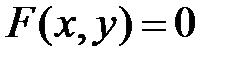, находят согласно правилу:

.

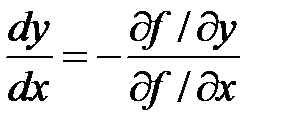Для функции 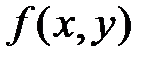определены производные второго порядка:

, , , .

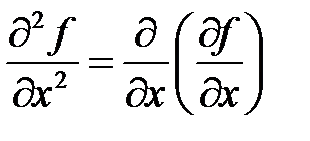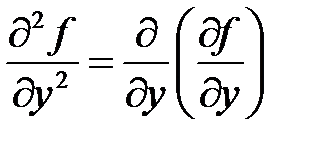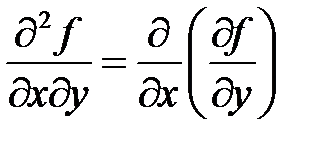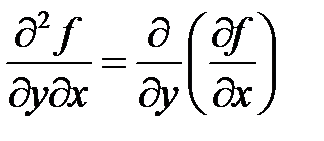Для функции 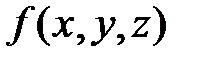, кроме указанных выше производных, определены следующие производные второго порядка:

, , , , .

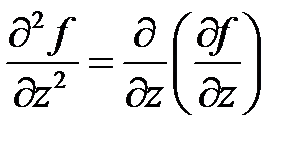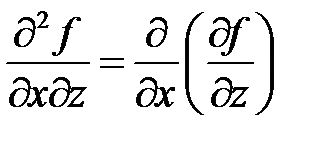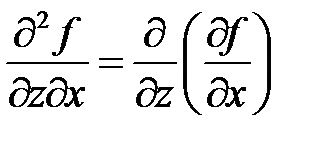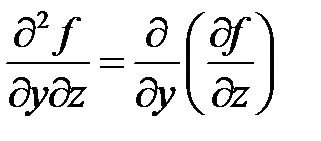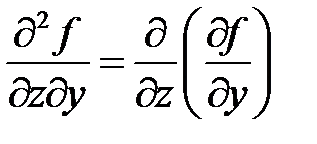Заметим, что в точках непрерывности смешанные частные производные равны.

Дифференциалы второго порядка определяются согласно соотношениям:

,

.

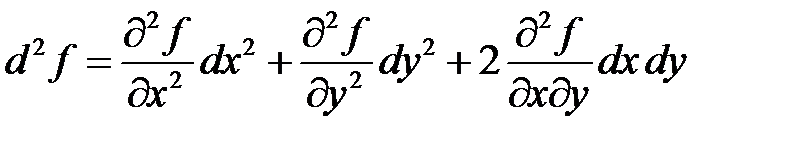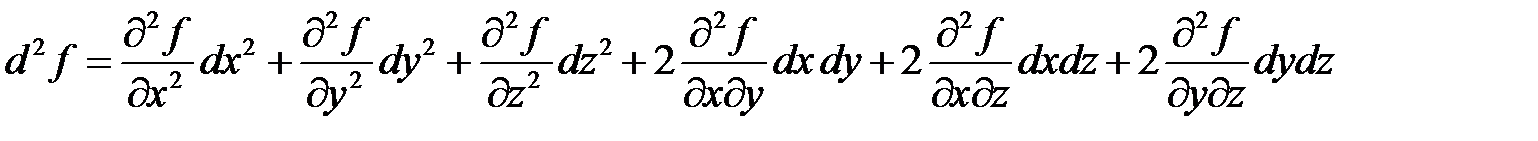Формула Тейлора в окрестности точки 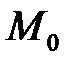с точностью до бесконечно малых второго порядка имеет вид:

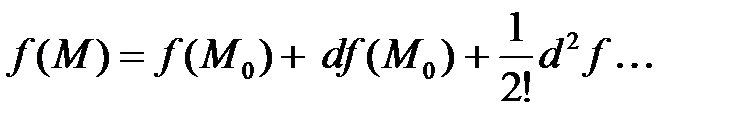
Точкой локального экстремума называют точку непрерывности функции 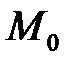, в окрестности которой приращение функции сохраняет знак: 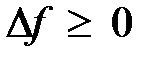- точка локального минимума, 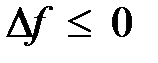- точка локального максимума. Необходимые условия существования экстремума записываются следующим образом:

,

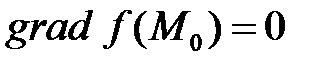что равносильно системе уравнений для нахождения критических точек функции:

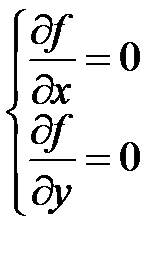или .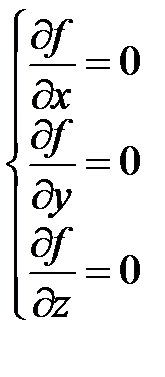

Достаточные условия существования экстремума определяются знаком приращения функции, который в свою очередь определяется знаком второго дифференциала:

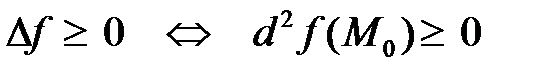, то точка является точкой локального минимума,

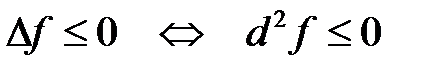, то точка является точкой локального максимума.

По своей структуре второй дифференциал является является квадратичной формой относительно дифференциалов 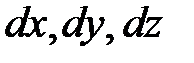и ему ставится в соответствие матрица:

.

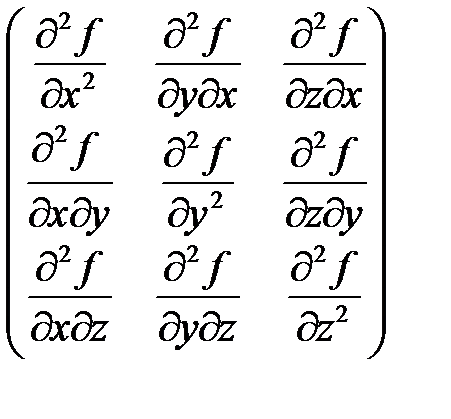Согласно критерию Сильвестра квадратичная форма является положительно определенной, если положительны все главные диагональные миноры этой матрицы:

, , .

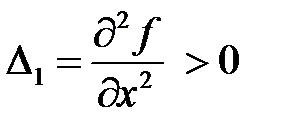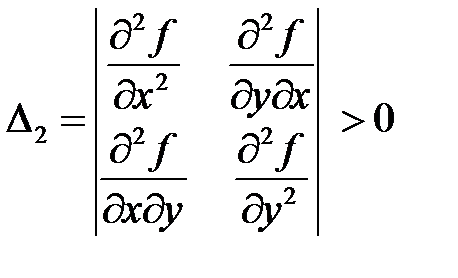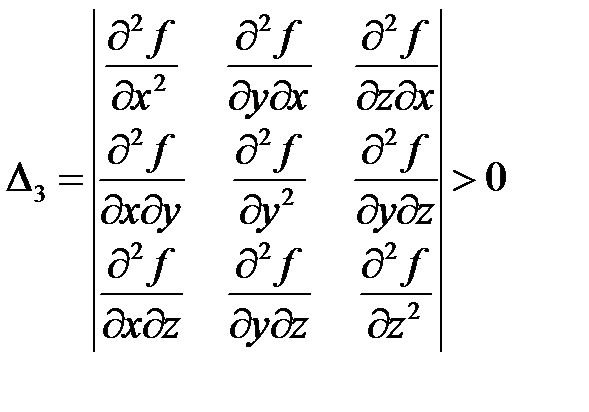(условия существования локального минимума), и является отрицательно определенной при условии 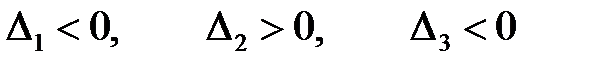(условия существования локального максимума).

Для нахождения точек условного экстремума исследуют на обычный экстремум функцию Лагранжа

.

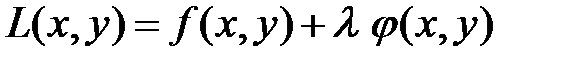Здесь 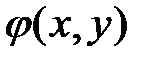- условие связи, а 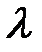- множитель Лагранжа. При этом достаточные условия существования экстремума выражаются через знак второго дифференциала 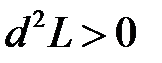(условие минимума), 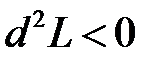- условие максимума. Знак второго дифференциала можно анализировать непосредственно при наличии условий связи.

Задачи

1. Запишите производные второго порядка для указанной функции, в указанной точке.

Запишите второй дифференциал.

Запишите матрицу, соответствующую d²f.

Запишите разложение по формуле Тейлора в указанной точке:

а)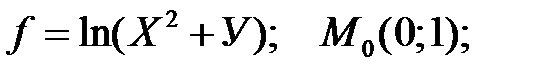

б)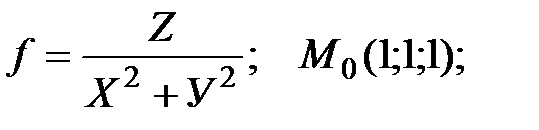

2. Исследуйте функцию на локальный экстремум:

а)	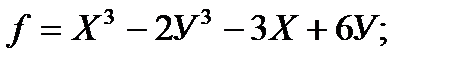б)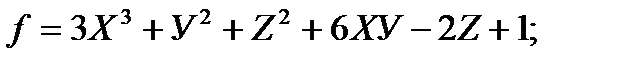
в)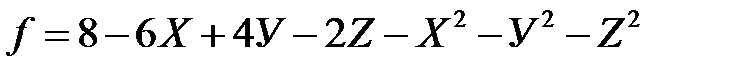

3. На эллипсоиде Х²+2У²+4Z²=8 найти точку, наиболее удалённую от М₀(0;0;3).

Date: 2015-09-24; view: 407; Нарушение авторских прав