Глава 9. Машины Тьюринга

Машина Тьюринга – это модель алгоритма, которая иллюстрирует процессы, происходящие при реализации алгоритма. Машина Тьюринга является гипотетической машиной. Ее составляют следующие компоненты.

· Управляющее устройство, которое в каждый данный момент времени может находиться в одном и только одном из некоторого множества состояний. Состояния обозначаются буквами так называемого внутреннего алфавита . Состояние 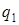, как правило, считают начальным состоянием, а состояние 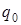– конечным (заключительным). Во внутренний алфавит включают также символы сдвига: 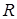– вправо, – влево, 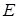– на месте.

· Лента, разделенная на ячейки и предполающаяся потенциально бесконечной в обе стороны (имеется в виду, что в каждый момент времени лента содержит конечное число ячеек, но при необходимости число ячеек можно увеличивать). В каждой ячейке может быть записан один и только один символ некоторого внешнего алфавита 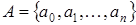. Символ принято считать пустым символом. Он обозначает пустую ячейку. По умолчанию, во всех ячейках, в которых не записаны символы 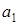, ,…, , 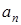записан символ . В данной главе в качестве внешнего алфавита мы будем рассматривать алфавит , 0 соответствует пустому символу.

· Считывающая и пишущая головка, которая в каждый данный момент времени обозревает одну ячейку.

…

…

…

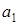
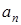
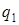
Рис. 1

Так, на рис. 1 считывающая головка обозревает ячейку ленты, в которой записан символ 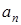. Управляющее устройство находится в состоянии 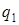(начальном состоянии). В зависимости от состояния управляющего устройства головка либо оставляет обозреваемый символ без изменения, либо записывает на его место любой другой символ внешнего алфавита, либо стирает обозреваемый символ. Далее головка либо остается на месте, либо передвигается на одну ячейку вправо или влево, при этом управляющее устройство переходит в некоторое новое состояние (состояние может и не меняться).

Каждое перемещение головки и изменение состояния управляющего устройства можно определить командой, которая обычно записывается в виде:

.

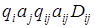Здесь:

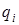· – состояние, в котором управляющее устройство находится в данный момент,

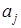· - символ, обозреваемый головкой,

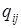· – состояние, в которое управляющее устройство переходит в зависимости от состояния 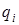и обозреваемого символа ,

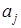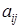· – новый символ, который записывается в ячейку, и зависящий от 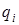и ,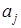

· – символ сдвига, указывающий направление движения головки (он также зависит от 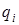и ).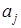

Список команд для машины Тьюринга называется программой. Существует взаимно однозначное соответствие между машинами Тьюринга и программами.

Вид ленты в каждый момент времени может быть определен конфигурацией вида:

.

Головкой в данный момент обозревается символ 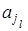, записанный в конфигурации первым справа от символа 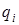. Первый и последний символы в данной конфигурации – непустые. Считается, что остальные символы на ленте, не записанные в конфигурацию – пустые. Имеется в виду, что в данный момент времени на ленте записано слово .

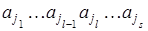Конфигурация, соответствующая началу работы машины, называется начальной. Если в процессе работы машина достигает заключительного состояния, то соответствующая конфигурация называется заключительной. Машина может прекратить работу и в случае, когда в программе отсутствует команда для некоторого состояния и некоторого символа.

Если машина Тьюринга 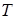, начав работу на некотором слове 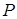, останавливается через некоторое число шагов, то считается, что она применима к слову 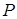. Результатом применения машины к слову является слово , которое соответствует заключительной конфигурации. Если же машина, начав работу на слове 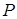, никогда не останавливается, то говорят, что она не применима к слову .

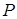Пример. Пусть машина Тьюринга задана программой:

.

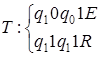Рассмотрим записанные в последовательных n ячейках n единиц.

Пусть, например, начальная конфигурация имеет вид:

.

Сокращенно эту конфигурацию можно записать так:

.

Вообще, записанные подряд n единиц обозначаются , а записанные подряд m нулей – .

Тогда в каждом такте машина Тьюринга будет оставлять обозреваемую единицу на месте и сдвигаться вправо на одну ячейку. Процесс будет продолжаться до тех пор, пока управляющая головка не выйдет на пустую ячейку (0). Здесь, согласно программе, в ячейку будет вписана единица, и машина остановится. В результате на ленте будет записано n +1 единиц. Если условиться, что исходное слово выражает число n, то можно считать, что машина вычисляет функцию .

Пример. Дана машина Тьюринга:

.

Выяснить, применима ли машина к слову :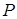

а) 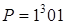; б) .

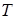Если применима, то выписать результат применения машины к слову 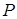. Предполагается, что в начальный момент времени головка машины обозревает самую левую единицу слова.

Решение. а) Применяя машину 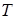к слову 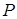, получаем последовательность конфигураций:

1) .	3) .
2) .	4) .

Вид второй конфигурации обусловлен тем, что символ 0 считается пустым символом и может не записываться.

Поскольку команда вида в программе отсутствует, то последняя конфигурация является заключительной. Следовательно, машина 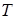к слову 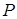применима, и 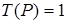. (Нули слева и справа от слова не записываются).

б) Получаем конфигурации:

1) .	6) .
2) 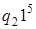.	7) .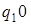
3) 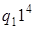.	8) .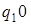
4) 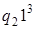.	9) .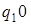
5) .	......

Процесс продолжается неограниченно, головка смещается по ленте вправо до бесконечности, следовательно, машина 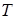к слову неприменима.

Вид конфигурации 8) обусловлен тем, что символ 0 (пустой символ) находится справа от последней единицы слова по умолчанию.

Машины Тьюринга и 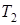называются эквивалентными, если:

· и 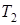либо обе применимы, либо обе неприменимы к каждому исходному слову ;

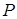· если обе машины применимы к слову 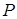, то .

Программу для машины Тьюринга можно задать не только с помощью последовательности команд, но и в виде таблицы. Так, в последнем примере программа может быть задана в виде:

		-

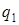
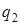
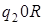
При табличной записи командой иногда называют выражение .

Имеет место следующий тезис.

Тезис Тьюринга. Всякий алгоритм может быть реализован соответствующей машиной Тьюринга.

Тезис является недоказуемым, так как он связывает нестрогое понятие алгоритма и строгое понятие машины Тьюринга.

Тезис может быть опровергнут построением примера алгоритма, который не может быть реализован машиной Тьюринга.

В Содержание.

Date: 2015-09-24; view: 883; Нарушение авторских прав