
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 6. Исчисление предикатов
|
|
Рассмотрим построение теории первого порядка.
Компонентами теории первого порядка являются следующие.
1. Алфавит составляют:
· Предметные константы – буквы начала латинского алфавита с натуральными индексами: 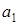 ,
,  , …,
, …,  ,
, 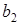 , … Предметные символы – это имена (обозначения) предметов.
, … Предметные символы – это имена (обозначения) предметов.
· Предметные переменные – буквы конца латинского алфавита с натуральными индексами:  ,
, 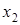 , …,
, …,  ,
,  , …
, …
· Функциональные буквы – строчные буквы латинского алфавита с натуральными индексами (верхний индекс указывает число переменных, нижний – номер функциональной буквы):  ,
, 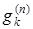 , …
, …
· Предикатные буквы – заглавные буквы латинского алфавита с натуральными индексами (верхний индекс указывает число переменных, нижний – номер предикатной буквы):  ,
, 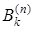 ,
, 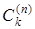 ,... (индексы можно не указывать).
,... (индексы можно не указывать).
· Логические связки: 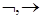 .
.
· Квантор всеобщности 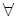 .
.
· Синтаксические символы – скобки (,) и запятая.
2. Формула определяется несколькими этапами. Вначале вводится понятие терма.
Определение. 1) Предметные константы и предметные переменные есть термы.
2) Если  ,
,  , …,
, …,  , – термы,
, – термы,  – функциональная буква, то
– функциональная буква, то 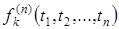 – терм.
– терм.
3) Символ является термом тогда и только тогда, когда это следует из 1) и 2).
Примеры. 1. Пусть  – предметная переменная,
– предметная переменная, 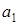 – предметная константа,
– предметная константа, 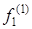 ,
,  – функциональные буквы. Тогда
– функциональные буквы. Тогда  ,
,  – термы.
– термы.
2. Пусть 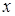 – предметная переменная,
– предметная переменная,  – предметная константа,
– предметная константа,  ,
,  – функциональные буквы. Тогда
– функциональные буквы. Тогда 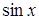 ,
,  – термы. Здесь символы
– термы. Здесь символы  ,
,  имеют только формальный смысл и не интерпретируются как обозначения тригонометрических функций.
имеют только формальный смысл и не интерпретируются как обозначения тригонометрических функций.
Определение. Если  ,
,  , …,
, …,  , – термы,
, – термы,  – предикатная буква, то символ
– предикатная буква, то символ  называется элементарной формулой.
называется элементарной формулой.
Другими словами, элементарная формула образуется при применении предикатной буквы к термам.
Примеры. 1. В условиях первого примера, если 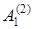 – предикатная буква, то
– предикатная буква, то 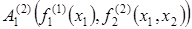 – элементарная формула.
– элементарная формула.
2. В условиях второго примера, если  – предикатная буква, то
– предикатная буква, то 
 – элементарная формула.
– элементарная формула.
Теперь определим формулу логики предикатов.
Определение. 1)Всякая элементарная формула есть формула.
2) Если  ,
, 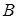 – формулы, то формулами являются также символы
– формулы, то формулами являются также символы 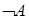 ,
, 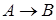 ,
, 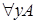 .
.
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).
Примеры. 1. В условиях первого примера,  – формула.
– формула.
2. В условиях второго примера, 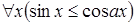 – формула.
– формула.
В теории первого порядка, как и в исчислении высказываний, допускаются формулы с другими логическими связками, а также допускается использование квантора существования. Известна формула (см. Глава 5. Предикаты.).
Здесь мы ненадолго отвлечемся от построения теории первого порядка и рассмотрим некоторые понятия, связанные с формулами.
Определение. Пусть  – формула,
– формула,  – переменная, которая входит в формулу
– переменная, которая входит в формулу  (один или несколько раз). Вхождение
(один или несколько раз). Вхождение  в формулу
в формулу  называется связанным, если либо
называется связанным, если либо  – переменная в кванторе (
– переменная в кванторе ( ), либо
), либо  находится в области действия квантора
находится в области действия квантора  . Если вхождение
. Если вхождение  в
в  не связано, то оно называется свободным.
не связано, то оно называется свободным.
Пример. В формуле  вхождения обеих переменных свободные.
вхождения обеих переменных свободные.
В формуле  вхождения переменной
вхождения переменной  в посылку связаны, а вхождение в следствие свободно. Вхождение переменной
в посылку связаны, а вхождение в следствие свободно. Вхождение переменной  свободно, так как отсутствует квантор
свободно, так как отсутствует квантор 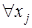 .
.
В формуле  вхождения обеих переменных связаны.
вхождения обеих переменных связаны.
Пусть  – формула,
– формула,  – переменная в формуле
– переменная в формуле  ,
,  – терм. Введем обозначение
– терм. Введем обозначение  . Тогда
. Тогда  – результат подстановки
– результат подстановки  вместо всех свободных вхождений
вместо всех свободных вхождений  в формулу
в формулу  .
.
Пример. Рассмотрим подстановку  вместо всех свободных вхождений
вместо всех свободных вхождений  в формулы из предыдущего примера.
в формулы из предыдущего примера.
В формуле  вхождение
вхождение  свободное, следовательно, получаем
свободное, следовательно, получаем  .
.
В формуле  вхождения переменной
вхождения переменной  в посылку связаны, а вхождение в следствие свободно. Получаем:
в посылку связаны, а вхождение в следствие свободно. Получаем:  .
.
В формуле  вхождения обеих переменных связаны, поэтому осуществить подстановку
вхождения обеих переменных связаны, поэтому осуществить подстановку  невозможно.
невозможно.
Определение. Терм  называется свободным для переменной
называется свободным для переменной  в формуле
в формуле  тогда и только тогда, когда никакое свободное вхождение
тогда и только тогда, когда никакое свободное вхождение  в формулу
в формулу  не лежит в области действия квантора
не лежит в области действия квантора 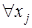 , где
, где  – переменная в терме
– переменная в терме  .
.
Пример. Рассмотрим формулу  и терм
и терм  .
. 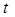 не свободен для переменной
не свободен для переменной 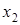 в данной формуле, так как
в данной формуле, так как 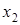 лежит в области действия квантора, тем более
лежит в области действия квантора, тем более 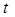 не свободен для переменной
не свободен для переменной  .
.
Пусть теперь дан терм 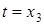 .
. 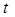 свободен для переменной
свободен для переменной 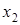 .
.
Уточним понятие интерпретации для множества формул  теории первого порядка.
теории первого порядка.
Определение. Интерпретацией множества формул  называется область интерпретации
называется область интерпретации  и заданное на ней соответствие, которое каждой предикатной букве
и заданное на ней соответствие, которое каждой предикатной букве  ставит в соответствие
ставит в соответствие  -местный предикат на
-местный предикат на  , каждой функциональной букве
, каждой функциональной букве  –
–  -местную функцию на
-местную функцию на  , каждой предметной константе
, каждой предметной константе 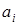 – элемент множества
– элемент множества  .
.
При интерпретации формулы превращаются в предикаты на множестве  . Если формула не имеет свободных переменных, то после интерпретации она превращается в высказывание.
. Если формула не имеет свободных переменных, то после интерпретации она превращается в высказывание.
Пример. На множестве  рассмотрим формулу
рассмотрим формулу 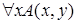 . Интерпретируем эту формулу следующим образом:
. Интерпретируем эту формулу следующим образом: 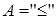 . Тогда мы получим предикат
. Тогда мы получим предикат 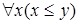 .
.
Рассмотрим теперь формулу  . При интерпретации она превращается в истинное высказывание
. При интерпретации она превращается в истинное высказывание 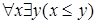 .
.
Определение. Интерпретация называется моделью формальной теории (или некоторого множества формул), если все формулы формальной теории (или множества формул) истинны в данной интерпретации.
Определение. Формула называется общезначимой (логически общезначимой), если она истинна в любой интерпретации.
Определение. Формулы  и
и 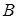 называются логически эквивалентными тогда и только тогда, когда формула
называются логически эквивалентными тогда и только тогда, когда формула 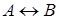 логически общезначима.
логически общезначима.
Справедлива теорема, аналогичная теореме из логики высказываний.
Теорема. Отношение логической эквивалентности является отношением эквивалентности.
Определение. Говорят, что формула  логически влечет формулу
логически влечет формулу 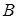 (из формулы
(из формулы  логически следует формула
логически следует формула 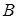 ), если формула
), если формула 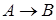 является логически общезначимой.
является логически общезначимой.
Теорема. Отношение логического следствия является отношением предпорядка.
Определение. Формула называется противоречивой, если она ложна в любой интерпретации.
Теорема. Пусть  – формула,
– формула,  – переменная в формуле
– переменная в формуле  , терм
, терм  свободен для переменной
свободен для переменной  в формуле
в формуле  . Тогда формула
. Тогда формула  общезначима.
общезначима.
Доказательство. Пусть имеется некоторая интерпретация исходной формулы, то есть множество  и
и 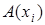 – предикат на
– предикат на  . Покажем, что
. Покажем, что 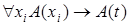 – тождественно истинный предикат. Возьмем произвольный набор значений
– тождественно истинный предикат. Возьмем произвольный набор значений 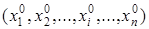 переменных
переменных  . Подставим этот набор в предикат. Получим высказывание:
. Подставим этот набор в предикат. Получим высказывание:

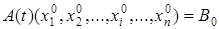 .
.
Покажем, что это высказывание истинно. Возможны два случая.
1. 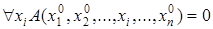 , следовательно
, следовательно 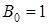 .
.
2. 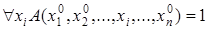 .
.
Соотношение выполнено при любых значениях  . Подставим этот набор значений в терм
. Подставим этот набор значений в терм  :
:  . Подставим последнее выражение в предикат
. Подставим последнее выражение в предикат  . Получим:
. Получим:
 .
.
Но, поскольку терм  свободен для переменной
свободен для переменной  в формуле
в формуле  , получаем:
, получаем:
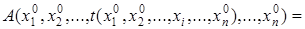
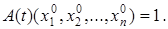
Следовательно, по свойству импликации получаем, что 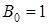 , что и требовалось доказать.
, что и требовалось доказать.
Теорема. Пусть  не является свободной переменной в формуле
не является свободной переменной в формуле  ,
, 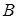 – некоторая формула. Тогда формула
– некоторая формула. Тогда формула  общезначима.
общезначима.
Доказательство аналогично доказательству предыдущей теоремы.
Теперь мы можем вернуться к построению теории первого порядка.
3. Аксиомы теории первого порядка делятся на два класса:
· Логические аксиомы:
1)  .
.
2) 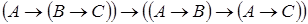 .
.
3) 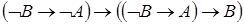 .
.
4) 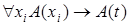 , где терм
, где терм  свободен для переменной
свободен для переменной  в формуле
в формуле 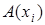 .
.
5)  , где
, где  – несвободная переменная в формуле
– несвободная переменная в формуле  .
.
Отметим, что аксиомы 1) – 3) – тавтологии, 4) и 5) – общезначимые формулы.
· Собственные аксиомы.
У каждой теории первого порядка свои собственные аксиомы.
4. Правила вывода.
1) Modus ponens (МР).
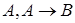 ├
├ 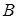 .
.
2) Правило обобщения Gen.
 ├
├  .
.
Определение. Теория первого порядка без собственных аксиом называется исчислением предикатов первого порядка (или чистым исчислением предикатов).
Без доказательства приведем теоремы.
Теорема. Всякая теорема исчисления предикатов логически общезначима, то есть исчисление предикатов непротиворечиво.
Теорема о полноте. Всякая логически общезначимая формула является теоремой исчисления предикатов.
Рассмотрим несколько примеров теорий первого порядка с собственными аксиомами, (приведем только собственные аксиомы). Для удобства вместо предикатных и функциональных букв будем записывать привычные символы.
Date: 2015-09-24; view: 1061; Нарушение авторских прав