Глава 8. Рекурсивные функции

Рекурсивные функции очень хорошо иллюстрируют понятие алгоритма. Если рассуждать упрощенно, то для рекурсивной функции должен существовать алгоритм, вычисляющей ее значения. Вообще говоря, большая часть известных числовых функций являются рекурсивными.

Полезно вспомнить, как определяются элементарные функции. Вначале рассматривается несколько классов функций: алгебраические, тригонометрические, показательные, логарифмические. Элементарная функция определяется как суперпозиция (или сложная функция) этих функций.

Рекурсивные функции строятся аналогичным образом.

Обратите внимание, что все функции в данном параграфе определены на множестве 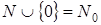. Если это необходимо, в обозначении функции верхний индекс указывает число переменных. Так, функция зависит от переменных. Таким образом, .

Рассмотрим вначале примитивно-рекурсивные функции.

Простейшие примитивно-рекурсивные функции задаются следующим образом.

· Функция следования задается формулой: (или ).

· Функция аннулирования задается формулой: .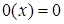

· Функция тождества определяется следующим образом: , то есть эта функция произвольному -мерному вектору сопоставляет его 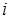-ю координату.

Из простейших примитивно-рекурсивных функций можно получить примитивно-рекурсивные функции с помощью следующих двух операторов.

· Оператор суперпозиции. Пусть , , , …, – примитивно-рекурсивные функции. Тогда функция

получена с помощью оператора суперпозиции.

Оператор суперпозиции – это оператор построения сложной функции. Если мы умеем вычислять функци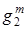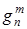и , , …, и , то значения функции 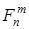могут быть получены последовательным вычислением значений функций , , 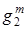…, 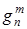на некотором наборе значений переменных , и вычислением значения функции на наборе значений , , …,

Пример. Функция получается суперпозицией функций 0(x) и s (x): . Аналогичным образом можно получить функции вида для всех значений n.

· Оператор примитивной рекурсии из известных примитивно-рекурсивных функци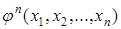й и позволяет строить новую функцию 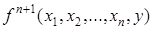. Так,

,

.

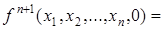
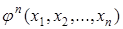Тогда функция 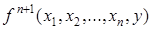получена с помощью оператора примитивной рекурсии, что выражается обозначением .

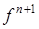Таким образом, сначала (при фиксированных значениях ) определяется значение функции при 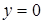, а затем каждое следующее значение функции (зависящее от 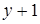) выражается через предыдущее значение (зависящее от ).

Пусть 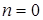. Тогда функция 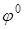есть постоянная. Обозначим ее следующим образом: 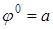. Функция 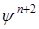зависит от двух переменных. Обозначим ее так: . Тогда

,

.

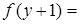
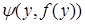Для произвольного получаем (обозначения 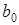, , , 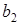…, вводятся в предположении, что набор фиксирован):

,

,

,

..................

.

..................

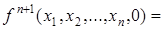
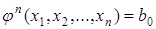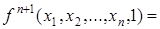
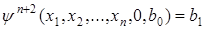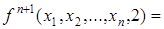
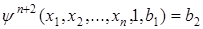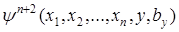Пример. Даны функции и 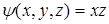. Определим функцию 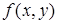, полученную из данных функций по схеме примитивной рекурсии.

Решение. Найдем значения функции .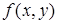

,

;

;

.

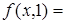
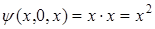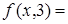
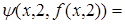
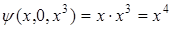Можно предположить, что .

Докажем последнюю формулу методом математической индукции по переменной .

1. Проверим формулу при .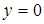

, то есть при 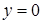формула верна.

2. Допустим, что предположение индукции верно при , то есть, верна формула .

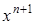Докажем, что предположение индукции верно при , то есть, верна формула 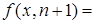. Выразим 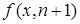с помощью схемы примитивной рекурсии.

.

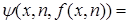
Таким образом, на основании метода математической индукции формула доказана для всех .

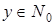Теперь строго определим примитивно-рекурсивные функции.

Определение. 1) Простейшие примитивно-рекурсивные функции примитивно-рекурсивны.

2) Примитивно-рекурсивными являются функции, полученные из примитивно-рекурсивных функций с помощью операторов суперпозиции и (или) примитивной рекурсии.

3) Функция является примитивно-рекурсивной тогда и только тогда, когда это следует из 1) и 2).

Пример. Покажем, что функция 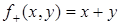примитивно-рекурсивна.

Доказательство. , , 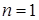следовательно, функция должна зависеть от одной переменной, а функция – от трех. Пользуясь заданием функции, найдем ее значения:

.

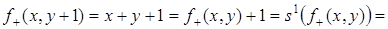
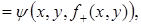
то есть .

Таким образом, функция 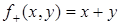получена по схеме примитивной рекурсии () из примитивно-рекурсивных функций, следовательно, сама является примитивно-рекурсивной.

Примитивно-рекурсивными, в частности, являются следующие функции: , , , , , ,

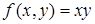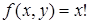Операция минимизации по 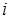-ой переменной функции обозначается следующим образом: , и определяется так.

Рассмотрим уравнение относительно :

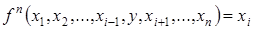. (1)

Это уравнение решается подбором, вместо переменной последовательно подставляются 0,1,2,… При этом возможны случаи.

· На некотором шаге левая часть соотношения (1) не определена. Следовательно, на наборе операция минимизации не определена.

· На каждом шаге левая часть соотношения (1) определена, но равенство не выполняется ни при каких значениях . Следовательно, на наборе операция минимизации не определена.

· Левая часть соотношения (1) определена при 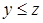, но при 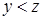равенство не выполняется, а при выполняется. В этом случае число 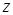считается значением операции минимизации на наборе .

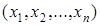Пример. [13]. Найти функции, получаемые из данной числовой функции с помощью оператора минимизации по каждой ее переменной.

Решение. Минимизируем функцию по переменной . Рассмотрим уравнение

. (2)

1. Если 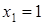, , то при подстановке 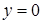получаем верное равенство.

2. Если , то левая часть равенства (2) не определена.

3. Если , , то при подстановке 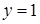в левой части равенства (2) появляется выражение 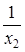, не имеющее смысла, и в этом случае операция минимизации не определена.

4. Если , то получаем равенство 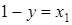. Оно имеет смысл при 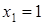, то есть 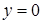, что рассмотрено в первом пункте, и при 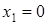, то есть 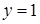. При 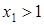равенство не имеет смысла.

Таким образом,

Минимизируем функцию по переменной 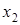. Рассмотрим уравнение

.

Это уравнение на самом первом шаге, при подстановке вместо нуля теряет смысл, значит, операция минимизации по второй переменной 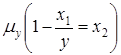нигде не определена.

Минимизируем функцию по переменной 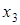. Рассмотрим уравнение

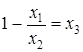. (3)

Если левая часть соотношения (3) имеет смысл и равенство (3) выполнено, то оно выполнено и при подстановке в это соотношение переменной на первом шаге, то есть при 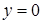. В остальных случаях значение операции минимизации не определено.

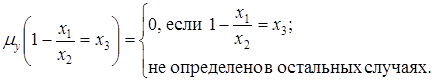
Определение. Частично-рекурсивной функцией называется числовая функция, получаемая за конечное число шагов из простейших примитивно-рекурсивных функций с помощью операторов суперпозиции, примитивной рекурсии и минимизации.

Определение. Числовая функция называется общерекурсивной, если она частично-рекурсивна и всюду определена.

Определение. Функция 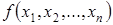называется эффективно вычислимой, если существует алгоритм, позволяющий вычислить ее значения.

В данном определении алгоритм понимается в интуитивном значении, следовательно, интуитивным является и понятие эффективно вычислимой функции.

Имеет место следующий тезис.

Тезис Черча. Каждая интуитивно вычислимая функция является частично-рекурсивной.

Тезис является недоказуемым, так как он связывает нестрогое понятие интуитивно вычислимой функции и строгое математическое понятие частично-рекурсивной функции.

Тезис может быть опровергнут построением примера интуитивно вычислимой, но не частично-рекурсивной функции.

В Содержание.

Date: 2015-09-24; view: 1236; Нарушение авторских прав