Сили, що діють на диполь. Енергія диполя в електростатичному полі

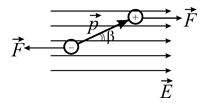Тепер помістимо диполь у зовнішнє електричне поле. Спочатку розглянемо найпростіший випадок однорідного поля. Де можна створити таке поле? У пласкому конденсаторі.

Нехай диполь розташований у електричному полі так, що дипольний момент утворює із вектором напруженості електричного поля кут 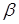. На позитивний заряд діє сила у напрямку вектора напруженості електричного поля, а на негативний – у протилежному напрямку. Очевидно, що на диполь діє пара сил, кожна з яких дорівнює 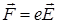. Вони будуть орієнтувати диполь відносно напрямку поля, тобто можна говорити про момент сили.

Момент сили за означенням визначається як векторний добуток сили на плече її прикладання. У випадку диполя плечем буде відстань між його зарядами 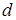. Момент цих сил становитиме

.

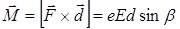Оскільки 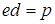за означенням дипольного моменту, то момент сили, що діє на диполь з боку електричного поля, дорівнює

.

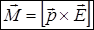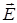Під дією цього моменту диполь буде намагатись орієнтувати свій момент паралельно вектору . Таке розташування диполя у електричному полі буде стійким. При відхиленнях від паралельного розташування дипольного моменту і поля виникне момент сил, що поверне диполь у вихідний стан. Розташування дипольного моменту проти поля є нестійким. Відхилення від паралельності викличе появу пари сил, що перевернуть дипольний момент у напрямку поля.

Давайте покажемо, що у рівноважному станові потенціальна енергія диполя мінімальна, тобто цей стан є енергетично вигідним. Диполь, орієнтований своїм моментом проти поля, буде мати максимальну енергію, його стан буде нестійкою рівновагою.

Прийнято вважати, що, коли дипольний момент перпендикулярний до поля, тобто кут 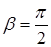, потенціальна енергія диполя в полі дорівнює нулю.

Тоді робота зміни кут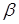а на 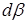є (згадайте з механіки)

.

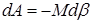Якщо 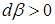, то робота, яка виконується, 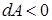, тобто робота виконується над диполем, а диполь набуває енергії. У випадку 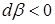, робота 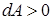, диполь сам виконує роботу, втрачаючи енергію.

Потенціальна енергія диполя при повороті на кут 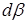зміниться на

.

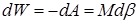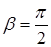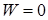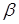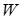Обертання диполя із стану, який характеризується кутом і потенціальною енергією до стану з довільними і дає

.

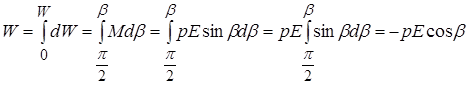Отриманий результат є не що інше як скалярний добуток дипольного моменту і вектора напруженості електричного поля, тому у більш загальному вигляді можна записати

.

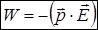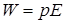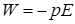Максимального значення енергія набуває при , а мінімального – при 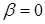. Власне, ми підтвердили з енергетичної точки зору, що розташування дипольного моменту у напрямку вектора напруженості електричного поля є стійким, оскільки йому відповідає мінімальна енергія.

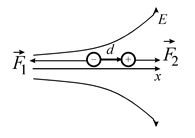Отриманий вираз справедливий не тільки для однорідного поля. Він є універсальним. Розглянемо диполь у неоднорідному вздовж осі 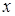електричному полі.

Будемо вважати, що дипольний момент розташований вздовж осі паралельно силовим лініям поля. Інші розташування поки що розглядати не будемо, оскільки все одно він повернеться у стійкий стан.

Нехай поле зменшується вздовж осі 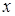. Тепер на заряди діятимуть різні сили 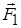і 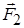, причому 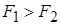. Це означає, що диполь буде втягуватись в ту частину поля, де вектор напруженості більше (на нашому рисунку він зміститься ліворуч). Саме цим пояснюється притягання легких предметів до наелектризованого тіла. У легких тілах індукуються заряди у вигляді диполів, і легке тіло зміщується у напрямку зарядженого тіла.

Знайдемо результуючу силу, внаслідок якої відбувається зміщення диполя. Будемо вважати, що довжина диполя дуже мала 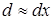, тобто маємо справу із так званим елементарним диполем. На негативний кінець диполя діє сила 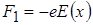, на позитивний – 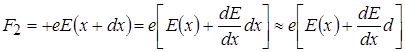. Тоді результуюча сила

.

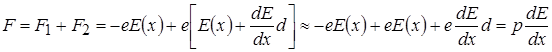Зверніть увагу, знак сили співпадає із знаком градієнту електричного поля. Оскільки у нас 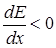(напруженість поля збільшується у напрямку, протилежному напрямку осі ), то і результуюча сила буде направлена у напрямку, протилежному осі . В загальному випадку для розташованого вздовж осі 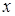диполя можна записати

.

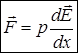Тепер знайдемо енергію диполя у неоднорідному полі. Візьмемо диполь і віднесемо його на нескінченність у напрямку осі 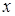. Вважатимемо, що на нескінченності поле відсутнє 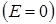, а потенціальна енергія диполя дорівнює нулю 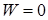(зверніть увагу: не тому, що диполь орієнтований перпендикулярно полю, а тому, що поля немає). Сила, що діє на диполь, направлена проти осі 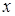, тому видалення диполя з точки 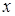на нескінченність вимагає витрати роботи

; .

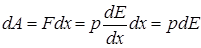Оскільки зміна енергії дорівнює виконаній роботі із протилежним знаком, тобто потенціальна енергія диполя

.

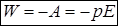Ми отримали такий самий вираз, як і для однорідного поля. Косинусу немає, оскільки ми із самого початку орієнтували диполь вздовж поля, тобто , .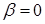

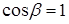В загальному випадку, коли напруженість електричного поля 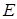залежить від координат 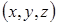, а диполь довільно розташований у просторі, так що проекції на осі вектора дорівнюють 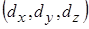, маємо

.

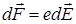Диференціал напруженості електричного поля

.

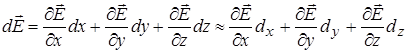Таке наближення припустиме у випадку елементарного диполя, тобто з малими розмірами 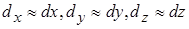. У такому наближенні сила набуває вигляду

.

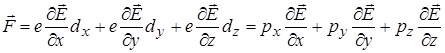Для скорочення запису візьмемо оператор набла

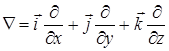
і скалярним множенням його да дипольний момент отримаємо новий оператор

.

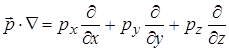За допомогою цього оператора сила записується як

.

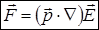Якщо диполь орієнтований вздовж напрямку вектора напруженості електричного поля, то 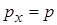, , 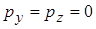отже маємо 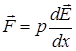, тобто результат попередньої задачі.

У цьому найзагальнішому випадку робота при переміщенні диполя у полі становить

,

де

.

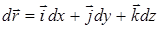Тоді

.

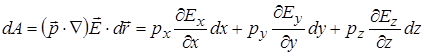Отриманий вираз є скалярним добутком

,

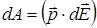отже при інтегруванні отримаємо

.

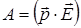Енергія дорівнює роботі із протилежним знаком, отже

.

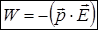Тепер можна вважати, що отриманий вираз для енергії диполя у електростатичному полі 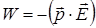є універсальним, який враховує і обертання диполя, і його втягування в ту частину простору, де напруженість поля більше.

Date: 2015-09-24; view: 811; Нарушение авторских прав